公式定義
 克拉莫-克若尼關係式
克拉莫-克若尼關係式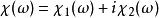 克拉莫-克若尼關係式
克拉莫-克若尼關係式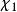 克拉莫-克若尼關係式
克拉莫-克若尼關係式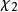 克拉莫-克若尼關係式
克拉莫-克若尼關係式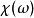 克拉莫-克若尼關係式
克拉莫-克若尼關係式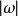 克拉莫-克若尼關係式
克拉莫-克若尼關係式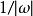 克拉莫-克若尼關係式
克拉莫-克若尼關係式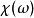 克拉莫-克若尼關係式
克拉莫-克若尼關係式給定一複數變數 的復值函式 ,其中 和 是實值函式。假設此函式 在複數平面上半部可析,且當 趨向無限大時,它在上半平面趨於零的速度比 快或與之相等,那么 滿足以下關係:
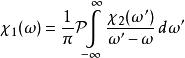 克拉莫-克若尼關係式
克拉莫-克若尼關係式和
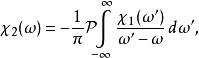 克拉莫-克若尼關係式
克拉莫-克若尼關係式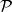 克拉莫-克若尼關係式
克拉莫-克若尼關係式其中 表示柯西主值。 因此可析函式的實部和虛部並不獨立:函式的一部分可以重建整個函式 。
推導
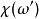 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式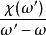 克拉莫-克若尼關係式
克拉莫-克若尼關係式推導克喇末-克勒尼希關係式是留數定理的基本套用。對任何復面上半可析函式和實數函式在復面上半可析。
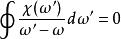 克拉莫-克若尼關係式
克拉莫-克若尼關係式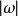 克拉莫-克若尼關係式
克拉莫-克若尼關係式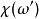 克拉莫-克若尼關係式
克拉莫-克若尼關係式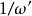 克拉莫-克若尼關係式
克拉莫-克若尼關係式選用實軸上的路徑、跳過任何實軸上極點、再以復面上半圓完成。把積分分解成三部分。其中半圓部分長度和成正比,因此只要消失比快,對半圓部分積分趨向零。因此積分只剩實軸上直線部和跳過極點的小半圓:
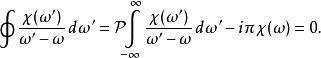 克拉莫-克若尼關係式
克拉莫-克若尼關係式以上第二項留數定理的結果。重組後得到克喇末-克勒尼希關係式:
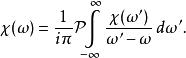 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式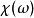 克拉莫-克若尼關係式
克拉莫-克若尼關係式分母里的虛數意味者這是連繫實部和虛部的公式。把分解成實部和虛部可輕易得到更早的公式。
物理理解
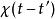 克拉莫-克若尼關係式
克拉莫-克若尼關係式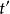 克拉莫-克若尼關係式
克拉莫-克若尼關係式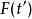 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式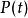 克拉莫-克若尼關係式
克拉莫-克若尼關係式可以將Kramers-Kronig關係套用於回響函式理論。物理上,回響函式概括系統對在時間的作用力在另一時間的反應:
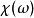 克拉莫-克若尼關係式
克拉莫-克若尼關係式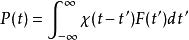 克拉莫-克若尼關係式
克拉莫-克若尼關係式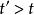 克拉莫-克若尼關係式
克拉莫-克若尼關係式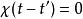 克拉莫-克若尼關係式
克拉莫-克若尼關係式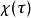 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式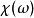 克拉莫-克若尼關係式
克拉莫-克若尼關係式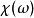 克拉莫-克若尼關係式
克拉莫-克若尼關係式因為系統不能在施力前有任何反應因此當,。 可以證明這因果關係意味著的傅立葉變換在復面上半可析。另外如果我們施加系統一個遠高於它最高共振頻率的高頻作用力,此時作用力轉換太快而系統不能即時做出反應,因此很大時,會趨近於0。從這些物理考量,可知物理反應函式通常符合克喇末-克勒尼希關係式的前提條件。
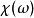 克拉莫-克若尼關係式
克拉莫-克若尼關係式反應函式的虛部和作用力異相。它概括系統如何消散能量。因此利用克喇末-克勒尼希關係,我們可以透過觀察系統能量消耗而得到它對作用力的同相(不做功)反應,反之亦然。
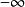 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式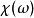 克拉莫-克若尼關係式
克拉莫-克若尼關係式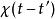 克拉莫-克若尼關係式
克拉莫-克若尼關係式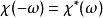 克拉莫-克若尼關係式
克拉莫-克若尼關係式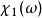 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式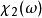 克拉莫-克若尼關係式
克拉莫-克若尼關係式 克拉莫-克若尼關係式
克拉莫-克若尼關係式上述函式的積分路徑是從到,其中出現了負頻率。幸運的是,多數系統中,正頻回響決定了負頻回響,這是因為是實數變數的傅立葉變換,根據對實數進行傅立葉變換的性質,,是頻率的偶函式,而是的奇函式。
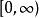 克拉莫-克若尼關係式
克拉莫-克若尼關係式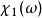 克拉莫-克若尼關係式
克拉莫-克若尼關係式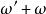 克拉莫-克若尼關係式
克拉莫-克若尼關係式根據該性質,積分可以從正負無窮區間約化為的區間上。考慮實部的第一個關係,積分函式上下同乘可得:
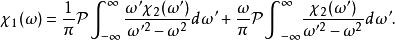 克拉莫-克若尼關係式
克拉莫-克若尼關係式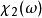 克拉莫-克若尼關係式
克拉莫-克若尼關係式由於為奇函式,第二項為零,剩下的部分為
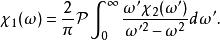 克拉莫-克若尼關係式
克拉莫-克若尼關係式類似的推導亦可用於虛部:
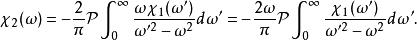 克拉莫-克若尼關係式
克拉莫-克若尼關係式該 Kramers-Kronig 關係在物理回響函式上的很有用處。
