光線跟蹤
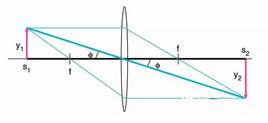
對於光學系統中的透鏡成像介紹,可以通過討論光線跟蹤開始。圖一是一個理想的薄透鏡對物體進行成像的基本光路圖。物體的高度為y1,到透鏡中心的距離為s1,透鏡的焦距為f。透鏡在另一端s2的位置成像,像高為y2。
 光學成像
光學成像對於理想的薄透鏡,它的厚度足夠薄,可以不計入焦距。這種情況下,穿過透鏡中心的光線發生的折射可以忽略。接下來的討論基於這種理想薄透鏡,這對於一些基本規律的討論是足夠的。透鏡的相差及厚度所產生的其他效應在這裡不加以考慮。
圖中包含三條光路,其中任意兩條都可以完全確定像的位置和大小。
最上面一條從物體發出並平行於透鏡的光軸,經過透鏡折射後穿過另一側的焦點。
第二條光束穿過透鏡左側的焦點,經過折射,與光軸平行。
第三條光束直接穿過透鏡中心。因為透鏡垂直於主光軸並且厚度很小,當光透過其中心時,折射可以忽略不計。
除了理想薄透鏡假設,還採用了近軸近似,也就是光線與光軸的夾角θ足夠小,可以把Sinθ近似為θ。
放大成像
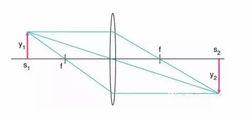
圖顯示了一個同樣的光路結構。從物體出發,穿過透鏡中心的光線與光軸成φ夾角,在透鏡兩側形成兩個相似三角形,
可以得到:φ= y1/s1 = y2/s2
進行變形得到:y2/y1 = s2/s1 = M
數值M即為透鏡對物體成像的放大倍數,同時也是像距和物距之間的比例。
 光學成像
光學成像這個比例關係對成像系統的結構構成了一個基本限制。對於一個給定尺寸的光學系統,要對物體產生特定放大倍數的成像,那么只有一個確定的透鏡位置才可以滿足要求。另一方面,成像系統的放大倍數不需要通過測量像和物體的尺寸來確定,它是由系統本身的結構決定的。
高斯透鏡方程
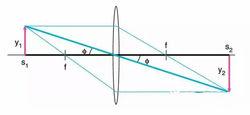
在圖中,從物體出發穿過前焦點的光束,與主光軸相交形成兩個相似三角形,頂角同為η,因此具有如下關係:y2/f = y1/(s1-f)
運用放大倍數的定義公式可以得到:y2/y1 = s2/s1 = f/(s1-f)
進行一下變形,最終我們得到1/f = 1/s1 + 1/s2
這就是高斯透鏡方程,它定義了透鏡焦距及成像系統尺寸之間的基本關係。這個方程與放大倍數的定義公式形成一個方程組,其中含有三個變數,焦距f,物距s1,以及像距s2。再加上另外一個條件方程就可以最終確定這三個變數。另外的一個條件通常是透鏡的焦距f,或者物像之間的距離,也就是s1+s2,它受系統的尺寸限制。任意一種情況都可以確定這三個變數。
 光學成像
光學成像光學不變數
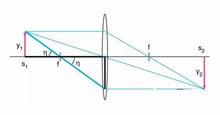
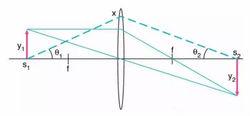
現在讓我們看一下物體發出的任意一條光束如何穿過系統。圖四顯示了一條從物體底部出發穿過透鏡頂端的光線,它和光軸之間具有最大的夾角。分析這條光束在光路設計中具有重要意義,在這裡它可以很好地演示任意光束是如何穿過系統的。
 光學成像
光學成像光束到達透鏡的位置與主光軸之間的距離為x。採用近軸近似並結合上面的公式,可以得到:θ1 = x/s1θ2 = x/s2 = (x/s1)(y1/y2)
變形得到:y2θ2 = y1θ1
這是光學成像的一條基本定律。在一個只由透鏡構成的光學系統中,像的尺寸與光束和光軸之間夾角的乘積是一個常數,稱之為光學不變數。
這個結果對任意個數的透鏡都是成立的,在一些光學著作中,也稱之為拉格朗日不變數或史密斯-亥姆霍茲不變數。
這個定律基於近軸近似和理想的無相差透鏡。如果考慮現實中透鏡的相差,上述方程中的等號需要換成大於等於號,也就是說相差可以使這個乘積有所增加,但沒有任何因素可以使它減小。