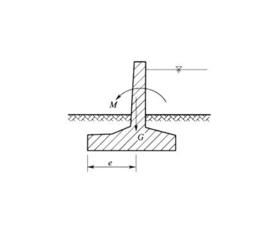
簡介
在建築工程中,磚混結構中的懸挑梁、懸挑陽台、擋土牆等有可能產生傾覆失穩的結構以及結構的抗震計算,均應進行傾覆驗算。與傾覆力矩相平衡的是抗傾覆力矩,只有當抗傾覆力矩大於傾覆力矩時結構才不會產生傾覆失穩。
計算公式
《抗規》6.1.3 的條文說明中規定框架部分地震傾覆力矩的計算公式為:
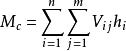 傾覆力矩
傾覆力矩其中,M為規定水平力下的地震傾覆力矩; n 為結構層數; m為框架 i 層的柱根數;V為第 i 層第 j 根框架柱計算地震剪力;h 為第 i 層層高。該條文說明中明確此框架部分按剛度分配的地震傾覆力矩的計算公式,為保持 2001 規範的規定不變,而 2001 規範給出此公式時並沒有具體說明公式來源。
規範目的
規範提出框架占整體抗傾覆彎矩比值的概念,主要是為確定框架與剪力牆的數量與比例關係,判斷結構整體變形與受力特徵,從而對於整體結構中的框架部分與剪力牆部分提出不同的抗震要求。對於層數較高的結構,無論是框架結構還是剪力牆結構,都會以整體的彎曲變形為主,原因是如果梁的剛度不夠,不能使結構形成整體彎曲變形,而僅依靠牆柱自身抗彎能力,整體變形狀態以剪下變形為主的話,其頂部位移指標等很難滿足要求。
而一般建築布置的情況都是框架柱在外圍,而剪力牆作為核心筒布置在結構中間部位,這就導致了在採用軸力方式計算時,框架所占比重遠大於剪力牆的情況,這時計算值會比較接近柱關於整體形心慣性矩占整體牆柱慣性矩的比例。如果梁剛度足夠大,則可以完全按格構柱模型,由平面牆柱布置來確定。
而抗規方法則有著比較明確的工程意義,一方面,將梁對整體結構的影響忽略了,或者說特意避開了,對豎向構件、牆、柱之間自身抗彎的比例關係做了一個分析。另一方面,作為抗震設計二道防線的要求,可以考慮在按強柱弱梁設計的結構,在出現梁鉸、梁退出結構整體剛度貢獻的時候,一個牆柱抗傾覆的比值。類似於疊合梁的概念,中間如果沒有抗剪作用的話,上下樑是相對獨立各自彎曲的,對整體的撓度抗彎能力沒有加強,當中間存在抗剪能力時,上下才會協同工作,形成整體剛度。當我們想比較的是上、下樑各自的相對的抗彎能力時,中間的抗剪作用是可以忽略的,這樣才更容易比較。
基於傾覆力矩的高層建築結構整體失效分析
高層建築結構在罕遇地震作用下,由重力二階效應引起的傾覆彎矩非線性遞增。當結構高度和高寬比不大時,附加彎矩對傾覆力矩的影響較小,可以忽略不計,但當結構高度和高寬比增大到一定限值時,二階效應引起的附加彎矩就成為了影響結構整體穩定的不可忽略的因素。雖然高層建築混凝土結構技術規程(以下簡稱高規)中給出了高層建築結構整體穩定性剛重比限值,但大量的實際工程指出結構即使滿足高規中對結構參數的規定,在結構剛重比不斷變化的結構失穩過程中,重力二階效應的影響仍然需要考慮,以此作為結構整體失穩的一個判別方面。
在對結構進行整體穩定分析時,由於對結構在材料非線性階段結構參數的變化規律不清楚,常常僅考慮彈性階段下結構整體穩定的設計參數,缺乏對結構塑性階段的研究。同時,按照傳統的結構設計理念,結構的失效模式認為結構的水平變形導致了結構的損傷,致使結構的抗側剛度退化,結構的頻率降低,當損傷達到一定程度時,即使很微小的變形也會引起極大的結構抗側剛度、基頻的變化,結構達到臨界失穩的界限,這種失效分析忽略了結構內部結構形式的多樣化,與實際工程實例中個別構件率先達到極限承載力而失去穩定不符。
對於高層建築結構,由於其高寬比較大,重力二階效應對其整體穩定的影響不可忽視。現有的結構整體穩定評價指標忽視了結構失穩的複雜性以及各狀態變數相互之間的關係,使得基於結構變形或抗側剛度等單一指標的失效判別指標偏不安全。因此,有必要尤其是從塑性階段結構傾覆力矩出發,建立一個基於傾覆力矩的整體失效的判別指標,從而為評估結構損傷以及整體穩定的發展提供依據。