簡介
當把置換寫成對換的乘積時,不要求(也不能要求)這些對換沒有公共的點,也不能保證表示的唯一性;甚至不能保證乘積中出現的對換的個數的唯一性。但是我們可以證明,當把一個置換 g 表示成對換的乘積,所需要的對換的個數的奇偶是被 g 完全確定的。一個可以表示成偶數個對換的乘積稱為偶置換(even permutation),否則稱為奇置換(odd permutation)。
性質
兩個偶置換的乘積,兩個奇置換的乘積都是偶置換。
一個偶置換和一個奇置換乘起來是奇置換。
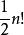 偶置換
偶置換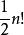 偶置換
偶置換若 |Ω|=n,則在Ω 的全體置換中,有個偶置換,有奇置換。
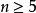 偶置換
偶置換全體偶置換在置換的乘法下成為一個群,稱為Ω 上的交錯群(alternating group),記作 Alt (Ω)。Alt (Ω) 是 Sym(Ω) 的正規子群。若 |Ω|=|Ω|,Sym(n) 或 S來表示 n 元集合上的對稱群。同樣用 Alt(n),或 A來表示 n 元集合上的交錯群。交錯群在有限群理論中具有重要地位。當時,A是單群。
置換群
[permutation group]
置換群是由置換組成的群。一個有限集合到自身的雙射稱為置換(permutation)。設 Ω 為有限集合,其元素按慣例稱為點。若α 為Ω 中一點,g 為Ω 一個置換,通常把α 在 g 下的像記作α 。設Ω={1,2,...,n},則 Ω 的置換可表成
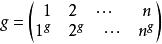 偶置換
偶置換的形狀,這裡把每個點的像寫在點的下方。
例如,Ω={1,2,3,4,5},
 偶置換
偶置換就表示這樣一個置換,它把 1 映成 2,把 2 映成 3,把 3 映成 1,把 4 和 5 互換。此時我們也把 g 寫作 g=(123)(45) 的形狀。
一般地,Ω={1,2,...,n} 上的任何置換都可以寫成
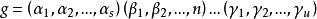 偶置換
偶置換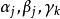 偶置換
偶置換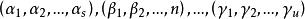 偶置換
偶置換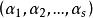 偶置換
偶置換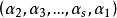 偶置換
偶置換的形狀,這裡 都是Ω 的點,而且Ω 的每個點在右端恰好出現一次。上面的寫法表示,g 把α 映成α,把α 映成α,...,又把α 映成α。同樣,g 把β 映成β ,把β 映成β,..., 又把β 映成β,等等。此處的 都稱為 輪換 (cycle),s,t,...,u 稱為它們的長度(length)。這種表示稱為置換的輪換分解(cycle decomposition)。在此分解中出現的各輪換的長度之和為Ω 的長度 n。按照上面的方法,(123)(45) 也可寫成(231)(54),或(312)(45),或(45)(231)等。這就是說,在輪換的分解中,各輪換的次序可以改變,同時輪換 也可用 代替。我們還規定,在用輪換分解來表示置換時,長度為 1 的輪換可以省略。
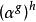 偶置換
偶置換若Ω 有 n 個點,則Ω 點置換共有 n!個。設 g,h 為兩個置換,它們作為映射可用相乘,把乘積記住 gh,點α 在 gh 下的像為。Ω 的全體置換在上述乘法下成為一個群,它稱為Ω 上的對稱群(symmetric group),通常記住 Sym(Ω)。Sym(Ω)的任意子群稱為Ω 上的置換群。
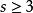 偶置換
偶置換長度為 2 度輪換稱為對換(transposition)。任何一個長度 2 的輪換可以寫成對換可以寫成對換的乘積。實際上,,有
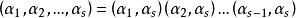 偶置換
偶置換。
進而每個置換都可以寫成對換的乘積。

