基本介紹
倉庫選用問題是一類混合整數規劃問題,決策者要在n個倉庫中決定選用哪幾個,以滿足m個顧客對貨物的需要,即每個顧客的需要量b(j=1,2,…,m)必須從各倉庫中得到滿足,且只能從動用的倉庫中得到滿足,而對動用的倉庫必須支付固定的費用(如租金、管理費等);同時,還應決定從動用的哪些倉庫中運多少貨物到顧客處,使總的耗費為最小 。
數學模型
倉庫選用問題的數學模型為:求一組變數x和y,使
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題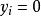 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題其中x表示從倉庫i運送給顧客j的貨物量, 表示倉庫i被動用, 表示倉庫i不被動用,g表示當使用倉庫i時的固定費用,d表示倉庫i的允許容量,c表示從倉庫i運送貨物到顧客j處的單位運費.由問題中的不等式約束條件,對於某個具體的i而言,當 時,y只能為1,即第i個倉庫被動用,其費用為
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題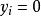 倉庫選用問題
倉庫選用問題當 時,y可能為0或1,但結合目標函式是求最小值,因而 。
例題解析
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題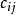 倉庫選用問題
倉庫選用問題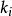 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題【例1】(倉庫選用問題)某公司擬在m個倉庫中決定租用其中的若干個,以滿足n個銷售點對貨物的需求,每個銷售點的需求量為 ,每個倉庫的庫容為 ,倉庫i到銷售點j的單位運費為 ,租用倉庫必須支付固定費用(如租金、管理費等) ,問選擇哪些倉庫,可滿足需求又能使總費用最小(假設 )?
 倉庫選用問題
倉庫選用問題解 設 表示從倉庫i到j的送貨量,那么,相應的費用為
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題其中
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題每一個倉庫有租用與不租用兩種可能,顯然, 時,不租用倉庫i, 時,則租用倉庫i,引入
 倉庫選用問題
倉庫選用問題上述費用可改為
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題還應滿足需求約束
 倉庫選用問題
倉庫選用問題和供應約束
 倉庫選用問題
倉庫選用問題因此,該問題的數學模型為
 倉庫選用問題
倉庫選用問題 倉庫選用問題
倉庫選用問題
