介紹
 保號性
保號性 保號性
保號性 保號性
保號性 保號性
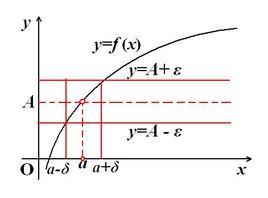
保號性函式 在一定點集 上有定義,且函式值恆正(或恆負),則稱函式 在一定點集 上具有保號性。
有界區域
函式有非零極限點去心鄰域內的局部保號性
 保號性
保號性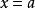 保號性
保號性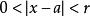 保號性
保號性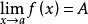 保號性
保號性定理 若函式 在 點的某個去心鄰域內 有定義,且 ,
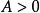 保號性
保號性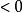 保號性
保號性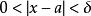 保號性
保號性 保號性
保號性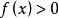 保號性
保號性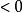 保號性
保號性(1)若 (或 ),則存在某個去心鄰域 ,對該去心鄰域內一切 恆有 (或 )。
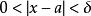 保號性
保號性 保號性
保號性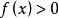 保號性
保號性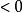 保號性
保號性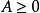 保號性
保號性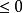 保號性
保號性(2)存在某個去心鄰域 ,對該去心鄰域內一切 恆有 (或 )。則 (或 )
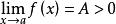 保號性
保號性證明(1)由於 ,根據極限定義,
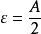 保號性
保號性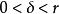 保號性
保號性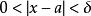 保號性
保號性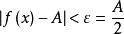 保號性
保號性對於取定正數 ,總存在 ,當 時,有 ,
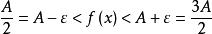 保號性
保號性 保號性
保號性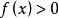 保號性
保號性即 ,該去心鄰域內一切 恆有 。
(2)是 (1)的逆否命題,用反證法可得證明。
函式連續點鄰域內的局部保號性
 保號性
保號性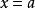 保號性
保號性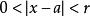 保號性
保號性 保號性
保號性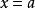 保號性
保號性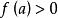 保號性
保號性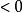 保號性
保號性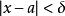 保號性
保號性 保號性
保號性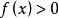 保號性
保號性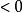 保號性
保號性若函式 在 點的某個去心鄰域內 有定義, 在 點連續,且 (或 ),則存在某個(實心)鄰域 ,對該去心鄰域內一切 恆有 (或 )。
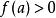 保號性
保號性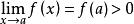 保號性
保號性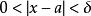 保號性
保號性 保號性
保號性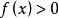 保號性
保號性證明 不妨設 ,根據連續定義,有 ,根據極限的局部保號性,知存在某個去心鄰域 ,對該去心鄰域內一切 恆有 。
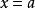 保號性
保號性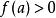 保號性
保號性 保號性
保號性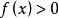 保號性
保號性由於該鄰域中心 點已有 ,該去心鄰域對應的實心鄰域內一切 恆有 。
無窮遠處
 保號性
保號性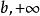 保號性
保號性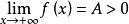 保號性
保號性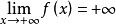 保號性
保號性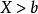 保號性
保號性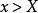 保號性
保號性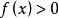 保號性
保號性若函式 在( )上有定義, 【或 】,則必存在 ,當 時, 。
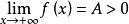 保號性
保號性結論1的證明對於 的情況 ,根據極限定義,
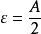 保號性
保號性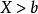 保號性
保號性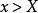 保號性
保號性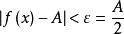 保號性
保號性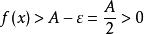 保號性
保號性對於取定正數 ,總存在 ,當 時,有 ,即 。
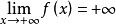 保號性
保號性 保號性
保號性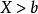 保號性
保號性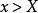 保號性
保號性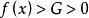 保號性
保號性對於 的情況,根據極限定義,對於任意取定的正數 ,必存在 ,當 時, 。
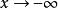 保號性
保號性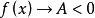 保號性
保號性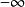 保號性
保號性對於 ,以及 【或 】的情況,都成立類似結論:
局部保序性
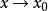 保號性
保號性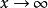 保號性
保號性局部保序性是函式極限的重要性質之一,它是局部保號性的一個推廣。以下只就 的情況作敘述, 時的情況完全類似,不再贅述。
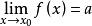 保號性
保號性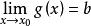 保號性
保號性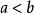 保號性
保號性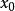 保號性
保號性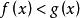 保號性
保號性定理 設 , ,若 ,則存在 點的某個去心鄰域,在此鄰域內恆有 。
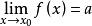 保號性
保號性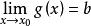 保號性
保號性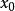 保號性
保號性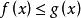 保號性
保號性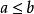 保號性
保號性設 , ,若存在 點的某個去心鄰域,在此鄰域內恆有 。則 。
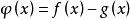 保號性
保號性這個定理可以直接證明,也可以作了輔助函式 後利用局部保號性來證明。
數列的保號性
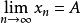 保號性
保號性若 ,
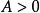 保號性
保號性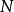 保號性
保號性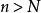 保號性
保號性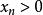 保號性
保號性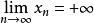 保號性
保號性(1)若 ,那么存在正整數 ,當 時,有 。【 注:若 也有類似結論】
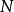 保號性
保號性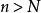 保號性
保號性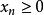 保號性
保號性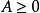 保號性
保號性(2)若存在正整數 ,當 時,有 ,則 。