簡介
保范同構亦稱等距同構映射,指兩個賦范線性空間之間存在保范同構映射。
保范映射
設X,Y是兩個賦范線性空間,U是X到Y的映射,若對一切x∈X,有||Ux||=||x||,則稱U是保范映射或等距映射。
定義
如果U不僅保范,而且還是從X到Y上的線性運算元,則稱U是X到Y上的保范同構映射。
如果空間X,Y之間存在一個保范同構映射,就稱X與Y保范同構,亦稱等距同構。
在巴拿赫空間理論中,常把保范同構的空間視為等同。
賦范線性空間
(normed linear space)
賦范線性空間是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量是完備的。
 保范同構
保范同構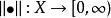 保范同構
保范同構 保范同構
保范同構定義:設是線性空間,函式稱為上定義的一個範數,如果滿足:
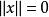 保范同構
保范同構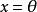 保范同構
保范同構(1)若且唯若;
 保范同構
保范同構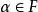 保范同構
保范同構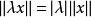 保范同構
保范同構(2)對任何及,;
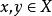 保范同構
保范同構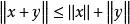 保范同構
保范同構(3)對任意,。
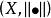 保范同構
保范同構稱二元體為賦范線性空間。
