伴隨陣

伴隨陣，又稱伴隨矩陣（adjoint matrix）。設R是一個交換環，A是一個以R中元素為係數的 n×n 的矩陣。A的伴隨矩陣可按如下步驟定義： 定義1：A關於第i 行第j 列的餘子式（記作Mij）是去掉A的第i行第j列之後得到的(n − 1)×(n − 1)矩陣的行列式。 定義2：A關於第i 行第j 列的代數餘子式是：Aij 。 定義：A的餘子矩陣是一個n×n的矩陣C，使得其第i 行第j 列的元素是A關於第i 行第j 列的代數餘子式。 引入以上的概念後，可以定義：矩陣A的伴隨矩陣是A的代數餘子矩陣的轉置矩陣： 也就是說， A的伴隨矩陣是一個n×n的矩陣（記作adj(A)），使得其第i 行第j 列的元素是A關於第j 行第i 列的代數餘子式。

定義

設A=(a)是n階方陣，由行列式|A|中的每個元素a的代數餘子式A所構成的矩陣

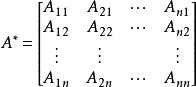伴隨陣

稱為矩陣A的伴隨矩陣。

註：伴隨矩陣A*在位置(i,j)上的元素是矩陣A在位置(j,i)上的代數餘子式。

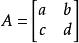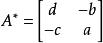伴隨陣

伴隨陣

例如，的伴隨矩陣是。

伴隨矩陣的性質

由伴隨矩陣的定義及轉置矩陣的定義，很容易得到下面的性質：

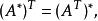伴隨陣

其中，A 表示矩陣A的轉置矩陣。由於矩陣kA的(i,j)元的代數餘子式為：

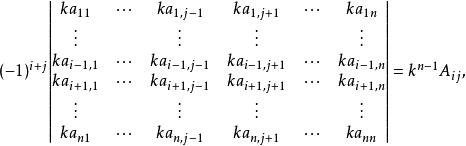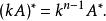伴隨陣

伴隨陣

因此，

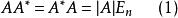伴隨陣

由伴隨矩陣的定義及矩陣的乘法運算馬上有下面的性質成立：

其中E為n階單位矩陣。

若n階方陣A是非奇異的，即|A|≠0，此時矩陣A是可逆的。由（1）得

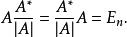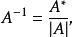伴隨陣

伴隨陣

結合逆矩陣的定義，有其中A 表示矩陣A的逆矩陣。

伴隨矩陣的求法:

主對角元素是將原矩陣該元素所在行列去掉再求行列式；

非主對角元素，是原矩陣該元素的共軛位置的元素去掉所在行列求行列式乘以(-1)^(x+y)，x,y為該元素的共軛位置的元素的行和列的序號，序號從1開始的。

主對角元素實際上是非主對角元素的特殊情況，因為x=y，所以(-1)^(x+y)=(-1)^(2x)=1，一直是正數，沒必要考慮主對角元素的符號問題。