條件
模型套用的條件:一個原來處於靜止狀態的系統,當系統中的物體間發生相對運動的過程中,有一個方向上動量守恆.
套用實例
1、“人船模型”
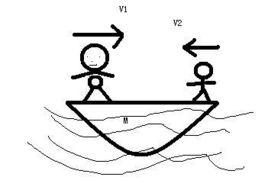
質量為M的船停在靜止的水面上,船長為L,一質量為m的人,由船頭走到船尾,若不計水的阻力,則整個過程人和船相對於水面移動的距離?
分析:“人船模型”是由人和船兩個物體構成的系統;該系統在人和船相互作用下各自運動,運動過程中該系統所受到的合外力為零;即人和船組成的系統在運動過程中總動量守恆。
解答:設人在運動過程中,人和船相對於水面的速度分別為v和u,則由動量守恆定律得:
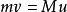 人船模型
人船模型由於人在走動過程中任意時刻人和船的速度v和u均滿足上述關係,所以運動過程中,人和船平均速度大小 也應滿足相似的關係,即
mv=Mu
而v=x/t,u=y/t,所以上式可以轉化為:
mx=My
又有,x+y=L,得:x=[M/(m+M)]L,y=[m/(m+M)]L
以上就是典型的“人船模型”,說明人和船相對於水面的位移只與人和船的質量有關,與運動情況無關。該模型適用的條件:一個原來處於靜止狀態的系統,且在系統發生相對運動的過程中,至少有一個方向(如水平方向或者豎直方向)動量守恆。
2、“人船模型”的變形
變形1:質量為M的氣球下掛著長為L的繩梯,一質量為m的人站在繩梯的下端,人和氣球靜止在空中,現人從繩梯的下端往上爬到頂端時,人和氣球相對於地面移動的距離?
分析:由於開始人和氣球組成的系統靜止在空中,豎直方向系統所受外力之和為零,即系統豎直方向系統總動量守恆。得:
x+y=L
這與“人船模型”的結果一樣。
變形2:如圖所示,質量為M的 圓弧軌道靜止於光滑水平面上,軌道半徑為R,今把質量為m的小球自軌道左測最高處靜止釋放,小球滑至最低點時,求小球和軌道相對於地面各自滑行的距離?
分析:設小球和軌道相對於地面各自滑行的距離為x和y,將小球和軌道看成系統,該
系統在水平方向總動量守恆,由動量守恆定律得:
mx=My
x+y=L
這又是一個“人船模型”。
(1) 關於“人船模型”
典型的力學過程通常是典型的模型所參與和經歷的,而參與和經歷力學過程的模型所具備的特徵,將直接影響著力學過程的發生,發展和變化,在將直接影響著力學過程的分析思路,在下列力學問題中我們將面臨著一個典型的“人船模型”。
問題:如圖—1所示,質量為M的小船長L,靜止於水面,質量為m的人從船左端走到船右端,不計水對船的運動阻力,則這過程中船將移動多遠?
分析思路: 1.分析“人船模型”運動過程中的受力特徵,進而判斷其動量守恆,得:
mv+Mu=0
2.在上式兩端同乘以時間,就可得到人,船相對於地面移動的距離S1和S2的關係為:
mS1=MS2
3.考慮到人、船相對運動通過的距離為L,於是得:
S1+S2=L
4由此即可解得人、船相對於地面移動的距離分別為 :
S人=ML/(M+m) S船=mL/(M+m)
人船模型”的幾種變例
①把“人船模型”變為“人車模型”。
變例1:如圖—2所示,質量為M,長為L的平板小車靜止於光滑水平面上,質量為m的人從車左端走到車右端的過程中,車將後退多遠?
解答:變例1中的“人車模型”與“人船模型”本質相同,於是直接得: S2= mL/(M+m)
②把水平方向的問題變為豎直方向。
變例2:如圖—3所示,總質量為M的氣球下端懸著質量為m的人而靜止於高度為h的空中,欲使人能完全沿強著地,人下方的繩至少應為多長?
解答:變例2中的h實際上是人相對於地的位移S1,而繩長則是人與氣球的相對位移L,於是有: h= L
可解得繩長至少為: L= h
③把直線運動問題變為曲線運動.
變例3:如圖—4所示,質量為M的物體靜止於光滑水平面上,其上有一個半徑為R的光滑半球形凹面軌道,今把質量為m的小球自軌道右測與球心等高處靜止釋放,求M向右運動的最大距離。
解答:變例3中小球做的是複雜的曲線運動,但只考慮其水平分運動,其模型例與“人船模型”相同,而此時的相對位移大小為2R,於是物體M沿水平而向右移動的最大距離為:
S2= ·2R
④把模型雙方的質量比變為極端情況.
變例:如圖—5所示,光滑水平桿上套有一個質量可忽略的小環,長L的強一端系在環上下,另一端連著質量為M的小球,今使小球與球等高且將繩拉直,當把小球由靜止釋放直到小球與環在同一豎直線上,試分析這一過程中小球沿水平方向的移動距離.
解答:變例4中環的質量取得某種極端的值: m→0
於是所求的小球沿水平方向移動的距離應為: S2= L→0