簡介
亥姆霍茲（von Helmholz, H.L.P.,1821~1894,德國人）定義了一個狀態函式：A=U-TS。A 稱為亥姆霍茲自由能（Helmholz free energy），是狀態函式，具有容量性質。
亥姆霍茲自由能的引出原因
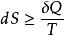亥姆霍茨自由能從熱力學第一定律和第二定律，我們分別得到了兩個狀態函式----內能和熵，為便於處理熱化學問題，定義了輔助狀態函式----焓。並得到了熵判據： 。
但用熵判據判斷過程的方向時，必須是隔離體系，或者是考慮環境的封閉體系，這很不方便。因此，有必要引入新的函式，利用體系自身的某種變化值判斷其自發變化的方向，而不用考慮環境。為此亥姆霍茲和吉布斯分別定義了兩個新的函式，這兩個函式和焓一樣，都是人為定義的輔助函式，不是熱力學定律的直接結果，但它們都是體系自身的性質，是狀態函式。
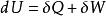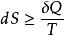亥姆霍茨自由能 亥姆霍茨自由能
亥姆霍茨自由能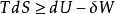
亥姆霍茨自由能結合第一定律 和第二定律 ，得 ，因T>0，故有： ，該式在不同的條件下，有不同的表現形式。
亥姆霍茲自由能和亥姆霍茲自由能判據
亥姆霍茲自由能：
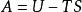亥姆霍茨自由能或
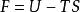亥姆霍茨自由能
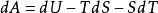亥姆霍茨自由能
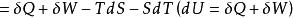亥姆霍茨自由能
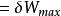亥姆霍茨自由能
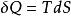亥姆霍茨自由能(等溫，可逆 )
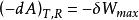亥姆霍茨自由能或 。
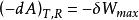亥姆霍茨自由能即：等溫、可逆過程中，體系對外所作的最大功等於體系亥姆霍茲自由能的減少值，所以把 A 稱為功函（work function）。若是不可逆過程，體系所作的功小於A 的減少值 。
如體系在等溫、等容且不作其它功的條件下
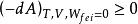亥姆霍茨自由能
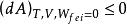亥姆霍茨自由能或 。
等號表示可逆過程，不等號表示是一個自發的不可逆過程，即自發變化總是朝著亥姆霍茲自由能減少的方向進行。這就是亥姆霍茲自由能判據。
此式的意義是：在等溫可逆過程中,封閉體系的亥姆霍茲自由能的減少等於體系對外所得做的最大功（含體積功和非體積功）。故亥姆霍茲自由能可視為等溫條件下體系作功的本領。這是該函式被稱為功焓的原因。若過程不可逆，則體系亥姆霍茲自由能的增加小於體系所獲得的功。因而,可用該式來判斷過程的方向性。
若體系經歷一個等溫等容過程，則：
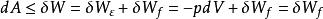亥姆霍茨自由能
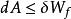亥姆霍茨自由能
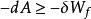亥姆霍茨自由能即： 。這說明在等溫等容過程中，體系亥姆霍茲函式的增加小於等於體系所獲得的非體積功，或體系亥姆霍茲函式的減少大於等於體系對外所做的非體積功( )。
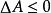亥姆霍茨自由能若體系在等溫等容且不做其它功的情況下，則： 。這就是亥姆霍茲自由能判據。
亥姆霍茲自由能和吉布斯自由能的區別
（1）亥姆霍茲自由能(Helmholtz free energy)：F=U-TS
U 是系統的內能，T 是溫度，S 是熵。
吉布斯自由能(Gibbs free energy)：G=H-TS
H為焓，S為熵，T為當前溫度。
由於吉布斯自由能 G 可以表示為 G = F + pV，另有G = μN，所以F = μN – pV；
（2）亥姆霍茲自由能的微分形式是：dF = - SdT -PdV + μdN，其中 P 是壓強，V 是體積，μ是化學勢，在統計物理學中，亥姆霍茲自由能是一個最常用的自由能，因為它和配分函式Z直接關聯：F = -kTlnZ
吉布斯自由能的微分形式是：dG = − SdT + Vdp + μdN，其中μ是化學勢，也就是說每個粒子的平均吉布斯自由能等於化學勢；ΔG叫做吉布斯自由能變（吉布斯自由能判據）。吉布斯自由能的變化可作為恆溫、恆壓過程自發與平衡的判據。吉布斯自由能改變數。表明狀態函式G是體系所具有的在等溫等壓下做非體積功的能力。反應過程中G的減少量是體系做非體積功的最大限度。這個最大限度在可逆途徑得到實現。
（3）反應進行方向和方式判據。（功函判據）
亥姆霍茲函式是一個重要的熱力學參數，等於內能減去絕對溫度和熵的乘積：兩個狀態差值的負數等於一個可逆等溫等容過程的最大功輸出。
亥姆霍茲自由能是等溫下做所有功的能力，亦稱功函。
吉布斯自由能是等溫等壓下除體積功以外的功的能力。
