空間交會對接
空間交會對接是指兩個太空飛行器在空間軌道上會合併在結構上連成一個整體的技術,是實現航天站、太空梭、太空平台和空間運輸系統的空間裝配、回收、補給、維修、航天員交換及營救等在軌道上服務的先決條件。它是載人航天活動的三大基本技術之一。
簡介
軌道交會是指2個運行在不同軌道上的太空飛行器在空間某點彼此接近的過程。通常在軌運行的太空飛行器並不需要進行軌道交會,甚至是要避免軌道交會。但是,隨著空間技術的不斷發展以及空間套用領域的拓展,軌道交會正逐漸成為許多空間任務執行過程中的重要環節,例如在軌服務、天基空間目標監視等。為了提高空間任務的執行效率,實現在軌多目標快速交會顯然非常有意義,尤其是針對不在同一軌道平面上的多顆衛星。
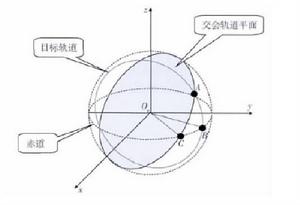
一般情況下,目標軌道是己知的,而交會軌道是未知的。但是,可以根據發射場位置、觀測條件等因素初步確定交會軌道的平面,即軌道傾角和升交點赤經。這時,就可以先確定目標衛星軌道與該軌道平面的交點,即穿越點。
共面橢圓交會軌道
空間交會一般指在任意軌道上運行的追蹤飛行器與目標飛行器在相同的時間到達相同的位置。軌道機動飛行器攜帶撞擊器運行在赤道大橢圓軌道上,而目標飛行器運行在任意軌道上,選擇目標飛行器軌道與赤道面的交點為預定交會點,實現赤道面內撞擊器與目標飛行器的橢圓軌道交會。這種交會是一種特殊交會。
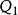 交會軌道
交會軌道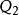 交會軌道
交會軌道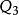 交會軌道
交會軌道若目標飛行器軌道傾角不為零,則選擇其軌道升交點 或降交點 作為預定交會點(如圖1所示,P點為軌道 機動飛行器變軌位置),目標飛行器過該點的時刻為交會時刻;若目標飛行器在軌道傾角為零的圓軌道上運行,則預定交會點可在圓軌道上隨意選擇,目標飛行器過預定交會點的時刻為交會時刻;若目標飛行器在傾角為零的橢圓軌道上運行,則選擇其軌道遠地點 作為預定交會點(如圖2所示,P點為軌道機動飛行器變軌位置),目標飛行器過該點的時刻為交會時刻。
對於運行在不同傾角軌道上的中、高軌目標飛行器,都可將預定交會點選在赤道面內。赤道大橢圓軌道機動飛行器與目標飛行器的遠程交會問題可表述為在赤道面內由大橢圓停泊軌道 出發,沿交會軌道在給定交會時刻到達預定交會點的固定時間共面橢圓交會問題,對應的交會軌道為與停泊軌道共面的橢圓軌道。在遠程交會段,軌道機動飛行器由地面導引逐漸接近目標飛行器,當軌道機動飛行器捕獲目標飛行器(與目標飛行器的距離小於200 km)時,認為遠程交會段結束,轉入近程交會段。
最優交會軌道規劃
對最優交會問題的研究始於20世紀60年代,眾多學者的關注與研究使該領域不斷發展,取得了很多理論與技術成果,在實際空間交會問題中發揮了理論指導與技術支撐作用。依照交會動力學進行分類,最優交會問題可分為線性交會問題與非線性交會問題。
對於橢圓交會軌道的遠程交會段與近程交會段,需要分別研究相應最優交會軌道規劃與制導方法,以獲得滿足各飛行階段軌道特性和各種路徑約束的最優交會軌道。在遠程交會段,兩飛行器相對距離大,一般基於慣性系中的絕對動力學方程,採用非線性軌道規劃與制導方法研究最優交會軌道。非線性軌道規劃與制導方法也可套用於近程交會段,但該階段軌道機動飛行器與目標飛行器的相對距離遠小於兩飛行器地心距離,可基於線性化相對運動方程,採用線性軌道規劃與制導方法研究最優交會軌道。
非線性最優交會軌道規劃與制導
非線性脈衝最優交會研究已有近百年的歷史,直到近年仍是一個主要研究方向,發展趨勢是採用的動力學模型和性能指標函式變得更複雜。
 交會軌道
交會軌道Hohmann研究了共面圓軌道間兩衝量最優交會解,Lambert給出了固定時間非共面軌道間兩衝量交會解,Prussing對Lagrange飛行時間定理中的兩個角度變數給出了幾何解釋,Battin利用超幾何級數法給出了經典Lambert問題的快速計算方法,趙瑞安對空間武器軌道設計中的經典Lambert問題進行了詳細介紹,並闡述了經典Lambert問題的Baton-Vaughan求解方法。兩衝量Hohmann交會與兩衝量Lambert交會都只進行了兩次軌道機動,燃料消耗不一定最優。Hughes等研究了二體方程下基於Lambert算法的多脈衝最優交會的參數最佳化模型和不同最佳化算法的最佳化性能。針對兩點邊值問題,Lawden提出主矢量理論研究最優飛行軌道,給出了脈衝最優交會軌道滿足的一階必要條件,該理論在固定時間多脈衝交會中具有非常重要的地位,適用於地球中心引力場中的最優飛行控制問題。Jezewski等給出了基於主矢量理論的多脈衝最優數值求解算法。Eckel研究了異面橢圓軌道多脈衝交會問題,結合主矢量理論和極大值原理推導了最優解滿足的條件。Jezewski基於主矢量方法和經典Lambert轉移,基於序列二次規划算法得到標稱解,並以標稱解為初值疊代得到了考慮地球非球形 項攝動的攝動解。Taur等採用主矢量方法研究了最小或最大轉移飛行半徑約束的共面圓軌道固定時間脈衝最優交會問題。Lion和Handelsman發展了主矢量理論,將主矢量推廣到非最優軌道,給出了多脈衝最優軌道改進方法。至今,基於非最優主矢量理論的非線性最優交會研究多集中在圓軌道交會問題,對橢圓軌道攔截問題的研究較少。
當交會採用比較複雜的動力學模型時,兩點邊值問題不能直接通過解析方法求解,此時的非線性最優交會多依賴於數值算法。Werner等給出了一種用於求解最優控制問題的數值算法。劉魯華和湯國建等用動態規劃原理實現了多衝量最優交會,從運籌學角度將多衝量最優交會問題轉化為多階段多維動態規劃問題,並著重對多階段二維動態規划進行分析研究,得到了兩衝量與三衝量交會問題最優解的求解算法。
雖然脈衝交會軌道在方案設計階段具有重要意義,但實際工程中也需要研究有限推力非線性最優交會軌道。發動機推力連續可變在工程上不易實現,研究中一般認為推力為有限常值。梁新剛和楊滌研究了一種套用非線性規劃求解有限推力作用下的異面最優軌道轉移方法,採用改進春分點根數形式的高斯行星方程將有限推力作用下異面最優軌道轉移問題最終轉化為針對協狀態初值等的參數最佳化問題。Fahroo基於Legendre偽譜法和非線性規划算法研究了有限推力最優交會問題,該方法比求解一般非線性規劃問題的計算量小。
線性最優交會軌道規劃與制導
線性交會與制導問題一般基於目標飛行器軌道坐標系中的相對運動方程進行研究,目標飛行器軌道偏心率直接影響相對動力學模型和相應的交會與制導方法。
當目標飛行器軌道為圓或近圓軌道時,線性化相對運動方程為一組常係數微分方程,具有形式簡潔的解析解,且解的精度足夠高,可以滿足交會動力學分析要求。Clohessy與Wiltshire基於圓參考軌道推導了著名的C-W方程,在相鄰圓軌道太空飛行器交會問題中得到了廣泛套用。Prussing基於C-W方程研究了相鄰圓軌道兩太空飛行器的線性最優交會策略,指出當交會時間在半個參考軌道周期以內,二脈衝最優解是最優解;當交會時間大於半個、小於兩個參考軌道周期時,三脈衝最優解是最優解;當交會時間大於兩個參考軌道周期時,四脈衝最優解是最優解,Prussing進一步指出對於線性最優交會,主矢量理論的最優交會必要條件同時也是充分條件,Stern、Neustadt分別用兩種方法證明了線性系統多脈衝最優交會次數最多為終端狀態數的結論,Jezewski}73' 74}基於C-W方程分別研究了燃料最優與時間最優交會問題,給出了解析分析方法,得到了與Lion等相似的結論。Carter研究了近圓共面四脈衝二次型最優交會問題,Luo等基於主矢量理論與進化算法,研究了共面圓軌道最優交會問題,得到了滿足最優一階必要條件的燃料最省交會軌道,許倫輝等基於線性相對運動方程,研究了交會對接尋的段最優衝量解的必要條件,推導了確定最優解主矢量曲線方程中待定參數的計算公式,給出了特定初始狀態和末狀態下實現遠距離接近的四次、三次和二次最優脈衝解的作用時刻和大小的算法,陳新海與陳文勝基於C-W方程研究了太空飛行器四衝量固定時間最優交會問題,給出了四脈衝最優點火時間、速度增量計算方法。