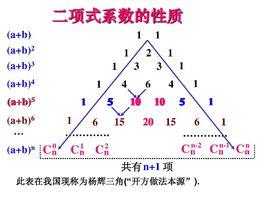
定義
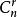 二項式係數
二項式係數一般二項式( x + y)ⁿ的冪可用二項式係數記為 。廣義二項式定理把這結果推廣至負數或非整數次冪,此時右式則不再是多項式,而是無窮級數。
二項式係數對組合數學很重要,因它的意義是從 n件物件中,不分先後地選取 k件的方法總數,因此也叫做 組合數。從定義出發,把 n個(1+ x)項的乘積展開,其中任意 k項的 x和 n− k項的1相乘得出一個 x,故此 x的係數是從 n個選取 k個的方法總數。把各項的 x標記可以更清楚看出:當 n=4, k=2時,
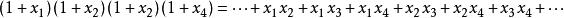 二項式係數
二項式係數, 所以 x的係數6等於從4項物件選取2項的方法總數。
二項式係數是楊輝三角的第 n+1行從左起第 k+1個數,它最先由楊輝發現。
二項式係數符合等式可以由其公式證出,也可以從其在組合數學的意義推導出來。如第一式左項表示從 n+1件選取 k件的方法數,這些方法可分為沒有選取第 n+1件,即是從其餘 n件選取 k件;和有選取第 n+1件,即是從其餘 n件選取 k−1件。而第二式則是每個從 n件選取 k件的方法,也可看為選取其餘 n− k件的方法。
發現歷程
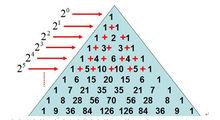 楊輝三角形
楊輝三角形二項式係數表為在我國被稱為賈憲三角或楊輝三角,一般認為是北宋數學家賈憲所首創。它記載於楊輝的《詳解九章算法》(1261)之中。在阿拉伯數學家卡西的著作《算術之鑰》(1427)中也給出了一個二項式定理係數表,他所用的計算方法與賈憲的完全相同。
在歐洲,德國數學家阿皮安努斯在他1527年出版的算術書的封面上刻有此圖。但一般卻稱之為帕斯卡三角形,因為帕斯卡在1654年也發現了這個結果。無論如何,二項式定理的發現,在我國比在歐洲至少要早300年。 1665年,牛頓把二項式定理推廣到n為分數與負數的情形,給出了展開式。 二項式定理在組合理論、開高次方、高階等差數列求和,以及差分法中有廣泛的套用。
性質
對稱性
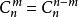 二項式係數
二項式係數與首末兩段“等距離”的兩個二項式係數相等。即。
單峰性
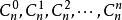 二項式係數
二項式係數是單峰序列。
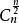 二項式係數
二項式係數(1)當n為偶數時,中間一項的二項式係數取得最大值。
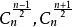 二項式係數
二項式係數(2)當n為奇數時,中間兩項的二項式係數相等且最大。
二項式係數的和
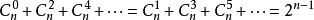 二項式係數
二項式係數二項式定理
二項式定理(binomial theorem),又稱牛頓二項式定理,由艾薩克·牛頓於1664、1665年間提出。
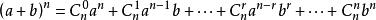 二項式係數
二項式係數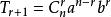 二項式係數
二項式係數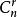 二項式係數
二項式係數此定理指出: ,通項公式為 其中, 叫做二項式係數。等號右邊的多項式叫做二項展開式。
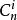 二項式係數
二項式係數其i項係數可表示為 ,即n取i的組合數目。 因此係數亦可表示為帕斯卡三角形(Pascal's Triangle)
二項式定理(Binomial Theorem)是指(a+b)ⁿ在n為正整數時的展開式。
排列與組合
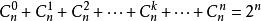 二項式係數
二項式係數1、
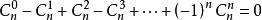 二項式係數
二項式係數2、
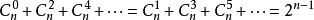 二項式係數
二項式係數3、
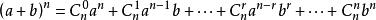 二項式係數
二項式係數證明:由
當a=b=1時,代入二項式定理可證明1
當a=-1,b=1時代入二項式定理可證明2
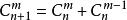 二項式係數
二項式係數4.組合數的性質: