歷史
楊輝三角形 主條目:楊輝三角形
二項式係數的三角形排列通常被認為是法國數學家布萊茲·帕斯卡的貢獻,他在17世紀描述了這一現象。但早在他之前,就曾有數學家進行類似的研究。例如,古希臘數學家歐幾里得於公元前4世紀提到了指數為2的情況。公元前三世紀,印度數學家青目探討了更高階的情況。帕斯卡三角形的雛形於10世紀由印度數學家大力羅摩發現。在同一時期,波斯數學家卡拉吉(英語:Al-Karaji)和數學家兼詩人歐瑪爾·海亞姆得到了更為普遍的二項式定理的形式。13世紀,中國數學家楊輝也得到了類似的結果。卡拉吉(英語:Al-Karaji)用數學歸納法的原始形式給出了二項式定理和帕斯卡三角形(巴斯卡三角形)的有關證明。艾薩克·牛頓勳爵將二項式定理的係數推廣到有理數。
定理的陳述
根據此定理,可以將 x+ y的任意次冪展開成和的形式
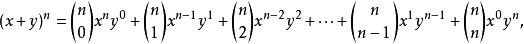 牛頓二項式
牛頓二項式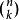 牛頓二項式
牛頓二項式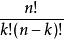 牛頓二項式
牛頓二項式其中每個 為一個稱作二項式係數的特定正整數,其等於 。這個公式也稱 二項式公式或 二項恆等式。使用求和符號,可以把它寫作
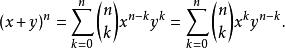 牛頓二項式
牛頓二項式後面的表達式只是將根據 x與 y的對稱性得出的,通過比較發現公式中的二項式係數也是對稱的。 二項式定理的一個變形是用 1 來代換 y得到的,所以它只涉及一個變數。在這種形式中,公式寫作
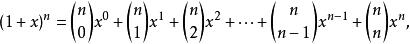 牛頓二項式
牛頓二項式或者等價地
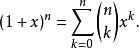 牛頓二項式
牛頓二項式套用[編輯]
牛頓以二項式定理作為基石發明出了微積分。其在初等數學中套用主要在於一些粗略的分析和估計以及證明恆等式等。
證明組合恆等式
 牛頓二項式
牛頓二項式二項式定理給出的係數可以視為組合數 的另一種定義。 因此二項式展開與組合數的關係十分密切。 它常常用來證明一些組合恆等式。比如證明
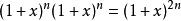 牛頓二項式
牛頓二項式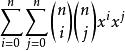 牛頓二項式
牛頓二項式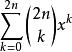 牛頓二項式
牛頓二項式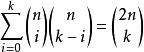 牛頓二項式
牛頓二項式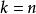 牛頓二項式
牛頓二項式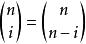 牛頓二項式
牛頓二項式可以考慮恆等式。 展開等式左邊得到:。 注意這一步使用了有限求和與乘積可以交換的性質。 同時如果展開等式右邊可以得到。 比較兩邊冪次為k的項的係數可以得到:。 令,並注意到 即可得到所要證明的結論。
多倍角恆等式
在複數中,二項式定理可以與棣莫弗公式結合,成為多倍角公式。根據棣莫弗公式:
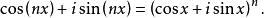 牛頓二項式
牛頓二項式通過使用二項式定理,右邊的表達式可以擴展為
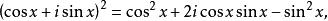 牛頓二項式
牛頓二項式由棣莫弗公式,實部與虛部對應,能夠得出
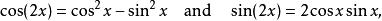 牛頓二項式
牛頓二項式即二倍角公式。同樣,因為
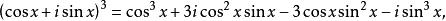 牛頓二項式
牛頓二項式所以藉棣莫弗公式,能夠得出
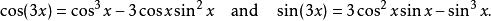 牛頓二項式
牛頓二項式整體而言,多倍角恆等式可以寫作
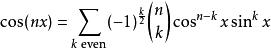 牛頓二項式
牛頓二項式和
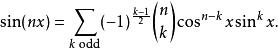 牛頓二項式
牛頓二項式e級數e
數學常數e的定義為下列極限值:
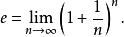 牛頓二項式
牛頓二項式使用二項式定理能得出
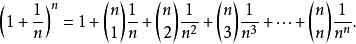 牛頓二項式
牛頓二項式第 k項之總和為
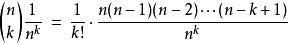 牛頓二項式
牛頓二項式因為 n→∞,右邊的表達式趨近1。因此
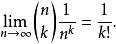 牛頓二項式
牛頓二項式這表明e可以表示為
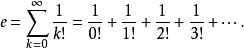 牛頓二項式
牛頓二項式推廣
該定理可以推廣到對任意實數次冪的展開,即所謂的牛頓 廣義二項式定理:
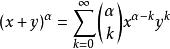 牛頓二項式
牛頓二項式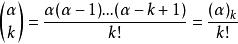 牛頓二項式
牛頓二項式。其中。
多項式展開
主條目:多項式定理
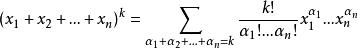 牛頓二項式
牛頓二項式對於多元形式的多項式展開,可以看做二項式定理的推廣:
.證明:
數學歸納法。對元數n做歸納:
當n=2時,原式為二項式定理,成立。
假設對n-1元成立,則:
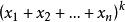 牛頓二項式
牛頓二項式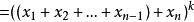 牛頓二項式
牛頓二項式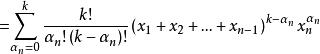 牛頓二項式
牛頓二項式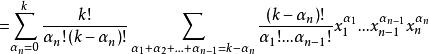 牛頓二項式
牛頓二項式 牛頓二項式
牛頓二項式證畢
