概述
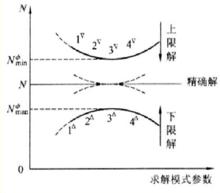圖1 精確解極限分析法最早由Drucker和Prager提出，是將物體的本構關係簡化為理想剛塑性應力–應變關係，利用剛塑性體處於極限狀態的普遍原理(上下限定理)求解極限荷載的一種分析方法。極限分析法中的上限定理和下限定理得到的是精確解答的上限和下限。
為了求得上限解，需要設定運動許可的速度場，凡是滿足速度邊界條件、幾何方程和體積不變條件的速度場，稱為運動許可的速度場。為了求得下限解，需要設定靜力許可的應力場，凡是滿足力平衡條件、應力邊界條件和不違背屈服準則的應力場，稱為靜力許可的應力場。精確解介於上限解和下限解之間，如圖1所示。如果上限解和下限解相等，它就是精確解。
定義
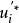上限法假設塑性變形區的位移狀態為動可容速度場 ，即滿足下列條件：
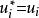上限法
上限法(1) 速度(位移)邊界條件： 或 ；
(2) 變形體內保持連續性，不發生重疊和開裂；
上限法
上限法(3) 體積不變條件： 或 。
由於所設的速度場只要求滿足動可容條件，而不考慮應力方面的條件，因此，該速度場不一定是真實速度場。所求得的載荷總是大於真實載荷，故稱為上限法。
上限法的原理
虛功原理
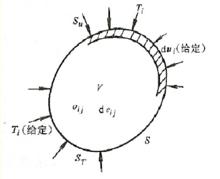圖2穩定平衡狀態的變形體中，當給予該變形體一幾何約束所許可的微小位移(因為該位移只是幾何約束所許可，實際上並未發生，故稱虛位移)時，則外力在此虛位移上所作的功(稱虛功)，必然等於變形體內的應力在虛應變上所作的虛應變功。
上限法
上限法圖2為變形體邊界的劃分及其上的表面力 和位移增量 。
虛功方程(基本能量方程)為：
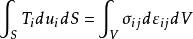上限法最大散逸功原理(第二塑性變分原理)
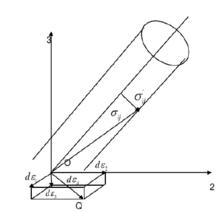圖3 主軸空間內的應力、應變矢量對剛塑性體一定的應變增量場而言，在所有滿足屈服準則的應力場中，與該應變增量場符合應力 應變關係的應力場所做的塑性功增量為最大。
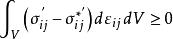上限法
上限法
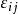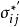上限法
上限法其中， 和 分別為符合應力應變關係的應力偏量和應變增量； 為滿足同一屈服準則的任意應力偏量。
上限法原理(上限定理)
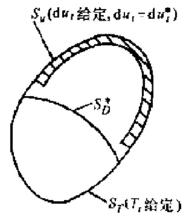圖4 上限定理邊界條件及速度間斷面示意
上限法
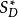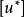上限法
上限法設有一動可容位移場 、速度間斷面 、位移增量間斷值，如圖4所示，則，由虛功方程得：
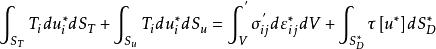上限法
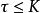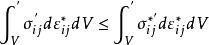上限法
上限法按屈服準則 ，由最大逸散功原理得： ；
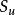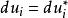上限法
上限法在 面上， ，由此可得上限定理的數學表達式：
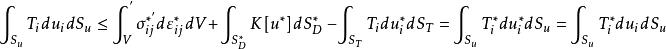上限法上限法的解題步驟
(1) 根據金屬流動模式(變形規律)和解題要求(如 缺陷分析)，設計動可容速度場；
(2) 利用塑性理論中的幾何方程，由該速度場確定應變速率場和等效應變速度場；
(3) 計算各項上限功率(虛應變功耗，接觸摩擦及剛性界面上剪下功耗等)；
(4) 利用最最佳化原理確定使總功率消耗為最小的準獨立變數；
(5) 求解上限載荷，並進行各變數間相互關係的分析，從中得出用以指導工藝變形的參數的結論。
上限法的特點
(1) 由於上限法所求得的載荷總是大於真實載荷，因此，對設備和模具比較安全；
(2) 上限法是利用能量平衡原理，不必解複雜的偏微分方程，計算比較簡單。
