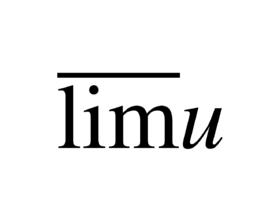定義
 上極限
上極限對一序列 ,令
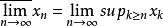 上極限
上極限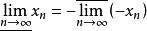 上極限
上極限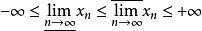 上極限
上極限(二者必定存在,且 )分別稱為當n→∞時,x的上極限與下極限。關於其他極限過程的上、下極限可類似定義。
數列上極限
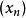 上極限
上極限給定無窮數列 ,它的一切收斂子數列的極限值的上確界值,稱為該無窮序列的上極限。
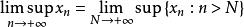 上極限
上極限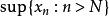 上極限
上極限或定義為 。因為 是遞減的,所以討論其極限值是有意義的。
集合上極限
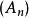 上極限
上極限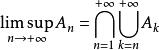 上極限
上極限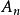 上極限
上極限給定無窮集合列 , 稱為無窮集合列的上極限集,含義為屬於無窮個 的元素組成的集合。
運算性質
在同一極限過程中下列式子成立:
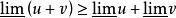 上極限
上極限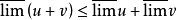 上極限
上極限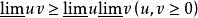 上極限
上極限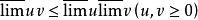 上極限
上極限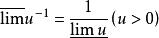 上極限
上極限若u存在,則上面的不等式成為等式。
比較性質
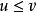 上極限
上極限若 ,則
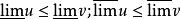 上極限
上極限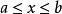 上極限
上極限若 ,a,b是常數,則
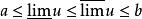 上極限
上極限與極限的關係
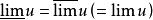 上極限
上極限lim u存在,則
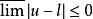 上極限
上極限lim u=l,則