基本介紹
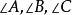 三角形元素
三角形元素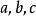 三角形元素
三角形元素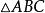 三角形元素
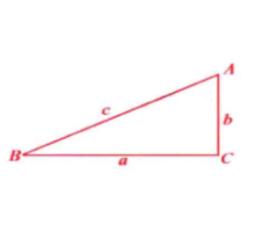
三角形元素一個三角形的邊、角、中線、高線、角平分線、周長、面積等都叫做三角形的元素。三角形的邊和角叫做 三角形的 基本元素。如右圖中的和它們的對邊是的基本元素。其它的的三角形元素稱為 三角形的非基本元素。
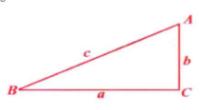 圖1
圖1重要的三角形元素
(1) 中線和重心:連線三角形的一個頂點與對邊中點的線段叫作中線,三角形內的三條中線的交點為重心。重心定理: 三角形的重心與頂點的距離等於它與對邊中點的距離的兩倍。
(2) 高和垂心:從三角形的一個頂點向對邊作垂線,頂點與垂足間的線段叫作三角形的高,三條高的交點叫作垂心。銳角三角形的垂心在三角形內,直角三角形的垂心就是直角頂點,鈍角三角形的垂心在三角形外。
(3) 角平分線和內心:三角形的一個內角的平分線與對邊相交,這個角的頂點與交點之間的線段叫作角平分線。三條角平分線的交點就是內心,也是三角形內切圓的圓心。對於角平分線,有性質:角平分線上的點到這個角的兩邊的距離相等。
(4) 外心:三角形外接圓的圓心也是三角形三邊垂直平分線的交點,由於垂直平分線上的點到線段兩端點的距離相等,所以外心到三角形三個頂點的距離相等。
(5) 中位線:連線三角形兩邊中點的線段叫作三角形的中位線,三角形的中位線平行於第三邊。並且等於它的一半 。
一般三角形的性質
(1) 三角形三邊的關係:三角形的任意兩邊之和大於第三邊,兩邊之差小於第三邊。
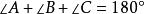 三角形元素
三角形元素(2) 三角形內角和定理:。
(3) 三角形的任意一個外角等於與它不相鄰的兩個內角的和;三角形的一個外角大於任何一個和它不相鄰的內角。
(4) 三角形面積公式:
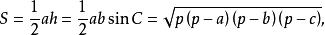 三角形元素
三角形元素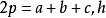 三角形元素
三角形元素 三角形元素
三角形元素(海侖公式),其中 是邊上的高,角C是a,b邊所夾的角,p為三角形的半周長 。