函式列及其一致收斂性
設
一致收斂判別法
一致收斂判別法
一致收斂判別法是一列定義在同一數集E上的函式，稱為定義在 上的函式列，簡記為 。
對於函式列，我們不僅要討論它在哪些點上收斂，而更重要的是要研究極限函式所具有的解析性質。比如能否由函式列每項的連續性判斷出極限函式的連續性。又如極限函式的導數和積分，是否分別是函式列每項導數或積分的極限。對這些問題的討論，只要求函式列在數集D上的收斂是不夠的，必須對它在D上的收斂性提出更高的要求才行，這就是以下所要討論的一致收斂性問題。
定義1
一致收斂判別法
一致收斂判別法
一致收斂判別法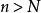
一致收斂判別法
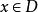一致收斂判別法設函式列 與函式 定義在同一數集D上，若對任給的正數 ，總存在某一正整數N，使得當 時，對一切 ，都有
一致收斂判別法 一致收斂判別法 一致收斂判別法則稱函式列 在D上一致收斂於 ，記作
一致收斂判別法 一致收斂判別法 一致收斂判別法
一致收斂判別法
一致收斂判別法 一致收斂判別法 一致收斂判別法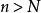 一致收斂判別法由定義可以看到，如果函式列 在D一致收斂，那么對於所給的 ，不管D上的哪一點 ，總存在公共的 （即N的選取僅與 有關，與 的取值無關），只要 ，都有
一致收斂判別法 一致收斂判別法 一致收斂判別法由此看到函式列 在D上一致收斂，必在D上的每一點都收斂。反之，在D上每一點都收斂的函式列 ，在D上不一定一致收斂。
定理1（函式列一致收斂的柯西準則）
一致收斂判別法 一致收斂判別法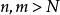
一致收斂判別法 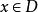一致收斂判別法函式列 在數集D上一致收斂的充要條件是：對任給正數 ，總存在正數N，使得當 時，對一切 ，都有
一致收斂判別法函式項級數及其一致收斂性
一致收斂判別法設 是定義在數集E上的一個函式列，表達式
一致收斂判別法
一致收斂判別法
一致收斂判別法稱為定義在E上的 函式項級數，簡記為 或 。稱
一致收斂判別法為函式項級數（2）的 部分和函式列。
一致收斂判別法若 ，數項級數
一致收斂判別法
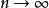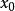一致收斂判別法
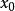一致收斂判別法
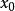一致收斂判別法 一致收斂判別法 一致收斂判別法 一致收斂判別法
一致收斂判別法收斂，即部分和 當 時極限存在，則稱級數（2）在點 收斂， 稱為級數（2）的收斂點。若級數（4）發散，則稱級數（2）在點 發散。若級數（2）在E上某個子集D上每點都收斂，則稱級數（2）在D上收斂。若D為級數（2）全體收斂點的集合，這時則稱D為級數（2）的收斂域。級數（2）在D上每一點 與其所對應的數項級數（4）的和 構成一個定義在D上的函式，稱為級數（2）的和函式，並寫作
一致收斂判別法即
一致收斂判別法也就是說，函式項級數（2）的收斂性就是指它的部分和函式列（3）的收斂性。
定義2
一致收斂判別法 一致收斂判別法 一致收斂判別法 一致收斂判別法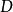 一致收斂判別法
一致收斂判別法 一致收斂判別法設 是函式項級數 的部分和函式列。若 在數集D上 一致收斂於 ，則稱 在 上一致收斂於 。
定理2（一致收斂的柯西準則）
一致收斂判別法 一致收斂判別法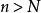 一致收斂判別法 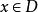一致收斂判別法
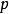一致收斂判別法函式項級數 在數集D上一致收斂的充要條件為：對任給的正數 ，總存在某正整數N，使得當 時，對一切 和一切正整數 ，都有
一致收斂判別法或
一致收斂判別法函式項級數的一致收斂性判別法
定理3（魏爾斯特拉斯判別法）
一致收斂判別法
一致收斂判別法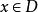 一致收斂判別法設函式項級數 定義在數集D上， 為收斂的正項級數，若對一切 ，有
一致收斂判別法 一致收斂判別法則函式項級數 在D上一致收斂。
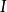一致收斂判別法下面討論定義在區間 上形如
一致收斂判別法的函式項級數的一致收斂性判別法，它與數項級數一樣，也是基於阿貝爾分部求和公式。
定理4（阿貝爾判別法）
設
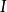一致收斂判別法 一致收斂判別法（i） 在區間 上一致收斂；
一致收斂判別法
一致收斂判別法（ii）對於每一個 ， 是單調一致有界的；
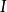一致收斂判別法 一致收斂判別法 一致收斂判別法（iii） 在 上一致有界，即對一切 和正整數n，存在正數M，使得
一致收斂判別法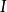 一致收斂判別法則級數（5）在 上一致收斂。
