公式定義
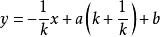一次函式垂線公式在平面直角坐標系xOy中，一次函式y=kx+b（k≠0），則其過A（a，ak+b）點的垂線的函式解析式為
推導過程
步驟1
求y=kx的過原點的垂線公式。
求y=kx的過原點的垂線公式。步驟2
由步驟一類推到y=kx過A（a，ak）的垂線公式。
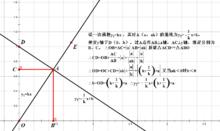y=kx過A（a，ak）的垂線公式。步驟3
進一步類推至y=kx+b過A（a，ak+b）的垂線公式。
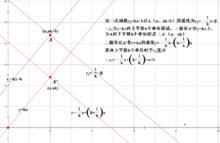y=kx+b過A（a，ak+b）的垂線公式。驗證
下載參考資料中幾何畫板檔案 。
請用幾何畫板軟體打開 一次函式垂線公式.gsp
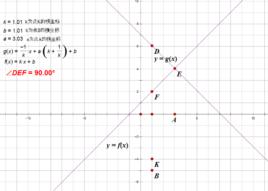
拖動點A，K，B，改變a、k、b的值。無論怎樣，都會發現兩函式之間的夾角∠DEF恆等於90°。
適用範圍
本公式適用於國中階段的平面直角坐標系中與直角三角形有關的問題。
例題套用
（2013鞍山）26．（10分）如圖，已知一次函式y=0.5x+2的圖象與x軸交於點A，與二次函式y=ax^2+bx+c的圖象交於y軸上的一點B，二次函式y=ax^2+bx+c的圖象與x軸只有唯一的交點C，且OC=2．
（1）求二次函式y=ax^2+bx+c的解析式；
（2）設一次函式y=0.5x+2的圖象與二次函式y=ax^2+bx+c的圖象的另一交點為D，已知P為x軸上的一個動點，且△PBD為直角三角形，求點P的坐標．
原題附圖過小無法直接上傳，圖片連結見 。
原版解法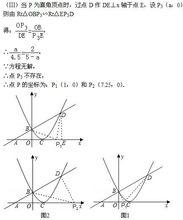
原版解法
原版解法運用垂線公式的解法（僅解第2小題）
解：（2）
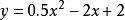一次函式垂線公式由（1）知二次函式解析式為
B（0,2）易得D（5,4.5）
分別代B、D點坐標和一次函式y=0.5x+2入垂線公式，直接解得P1（1,0）； P2（7.25,0）
P3求法與原版解法相同。
聲明
本公式純原創，公式作者為本詞條的創建者。本著方便大家做題與實際套用故發表到網上。本公式並不是已被教科書認可的公式，所以解題時不能用於解答題， 只能用於選擇、填空等不需寫明解題過程的題目。本公式的其他證法歡迎大家討論。
附：參考資料中有作者編輯的一次函式垂線公式的幾何畫板檔案。
