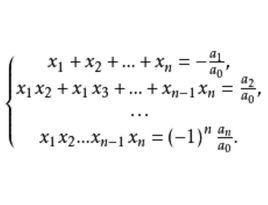基本介紹
如果f(x)是一元n次多項式，那么f(x)=0叫做一元n次方程，一元n次方程的一般形式是：
f(x)=axⁿ+a-xⁿ +…+ax+a=0 (其中a≠0，n∈N.)……①
當n>2時，稱為一元高次方程。
(1)若a(i=0，1，2，…，n)是複數，則稱方程為復係數一元n次方程，n>2時為復係數高次方程。
(2)若a(i=0，1，2…，n)是實數(或有理數、整數)，則稱方程①為實係數(或有理係數、整係數)一元n次方程.n>2時，也稱實係數(或有理係數、整係數)高次方程.。
(3)如果有α，使得f(α) =0，則α是方程f(x)=0的根 。
一元n次多項式的解
一元一次方程、一元二次方程、一元三次方程分別有一個根、二個根、三個根，它們都可以用代數解法來解，並且有求根公式。可以證明一元四次方程有四個根，並且可以用代數解法求解。 當n > 4時，根據伽羅華理論， 一般形式的n次方程不能用代數解法來解 。
關於一元n次方程的根的個數，我們有以下定理和推論。
定理1 (代數基本定理)一元n次方程至少有一個根。
如果f (x )的次數大手1, 那么根據定理1可以知道，方程f (x) =0至少有一個根，設這個根是α，那么由於f(α) =0，根據因式定理可以知道， f(x)=(x-α)q(x).，因為x-α和q (x)的次數都低於f(x)的次數，所以f(x)可約，由此我們得到:
推論1 任何次數大於1的多項式都是可約的 。
推論2 f(x)=axⁿ+axⁿ +…+ax+a=0 (其中a≠0，n∈N)的標準分解式是
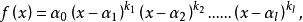一元n次方程
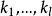一元n次方程
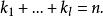一元n次方程式中 都是正整數，
根據f (x)的標準分解式可以知道，如果x=α(i=1,2,...,),那么f(α) =0,所以α是方程f(x)=0的根。這就是說，f(x)的毎一個一次因式的根都是方程f(x)=0的根，如果x-α是f (x)的k重因式，那么就說α是方程f(x)=0的k重根，在討論根的個數吋，k重根當作k個計算。
例如，方程(x-2) (x+1) (x-1)=0有三重根2，二重根-1，単根1，因此，這個方程一共有6個根。
定理2一元n次方程有n個根並且只有n個根。
證根據定理1的推論2，任何一個一元n次方程f(x)=0，如果把f(x)分解成標準分解式，就得
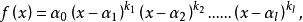一元n次方程 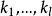一元n次方程 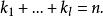一元n次方程式中 都是正整數，
因為方程有k重根α,k重根α,..., k重根α，共 有k+k+...+k=n個根，又因為f (x)的標準分解式是唯一的，所以f(x)=0有n個根並且只有n個根。
下面是一元n次方程的根和係數的關係的定理。
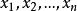一元n次方程定理3 (韋達定理)如果一元n次方程f(x)=axⁿ+axⁿ +…+ax+a=0 (其中a≠0，n∈N)的根是 ，那么
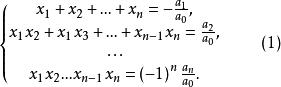一元n次方程 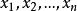一元n次方程 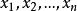一元n次方程韋達定理的逆定理也成立，也就是說，如果n個數 滿足關係式（1），那么 必為方程f(x)=axⁿ+axⁿ +…+ax+a=0 (其中a≠0，n∈N)的n個根 。
一元一次方程ax+b=0(a≠0)的解為
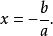一元n次方程韋達(Viete)給出了一元二次方程ax +bx+c=0(a≠0)的一個求根公式為
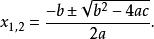一元n次方程一元三次方程有三個根，有可能都是實數根，也有可能是一個實數根和兩個互為共軛的複數根，不過，16世紀的數學家還沒有虛數的概念 。
一元四次方程由費拉里(Ferrari)解決，方法是將一元四次方程化為兩個一元二次方程與一個一元三次方程求解。
拉格朗日發現不能用求一元二次方程、一元三次方程、一元四次方程的方法來求解一元五次和一元五次以上的代數方程。
魯菲尼(Ruffini)-阿貝爾(Abel)定理：一般地，五次和五次以上的代數方程是不可能由代數根式求解。
伽羅瓦(Galois)建立了一般的理論：五次和五次以上方程代數可解的判別準則，伽羅瓦為群論奠定了基礎，群論在物理學中被用來研究對稱性 。
