發展歷史
隨著科學技術的日益發展,許多工程的核心問題最終都歸結為最佳化問題。因此,最最佳化已經成為工程技術人員必不可少的計算工具。在計算機已經廣為普及的今天,一些大規模的最佳化問題的求解可以在一台普通的計算機上實現,使得最最佳化方法得到了比以往任何時候都更加廣泛的套用。如今,最最佳化方法已成為工程技術人員所必需具備的研究工具。
常見方法
1. 梯度下降法(Gradient Descent)
梯度下降法是最早最簡單,也是最為常用的最最佳化方法。梯度下降法實現簡單,當目標函式是凸函式時,梯度下降法的解是全局解。一般情況下,其解不保證是全局最優解,梯度下降法的速度也未必是最快的。梯度下降法的最佳化思想是用當前位置負梯度方向作為搜尋方向,因為該方向為當前位置的最快下降方向,所以也被稱為是”最速下降法“。最速下降法越接近目標值,步長越小,前進越慢。
2. 牛頓法(Newton's Method)和擬牛頓法(Quasi-Newton Methods)
牛頓法
牛頓法是一種在實數域和複數域上近似求解方程的方法。方法使用函式f(x)的泰勒級數的前面幾項來尋找方程f(x) = 0的根。牛頓法最大的特點就在於它的收斂速度很快。
擬牛頓法
擬牛頓法是求解非線性最佳化問題最有效的方法之一,其本質思想是改善牛頓法每次需要求解複雜的Hessian矩陣的逆矩陣的缺陷,它使用正定矩陣來近似Hessian矩陣的逆,從而簡化了運算的複雜度。擬牛頓法和最速下降法一樣只要求每一步疊代時知道目標函式的梯度。通過測量梯度的變化,構造一個目標函式的模型使之足以產生超線性收斂性。這類方法大大優於最速下降法,尤其對於困難的問題。另外,因為擬牛頓法不需要二階導數的信息,所以有時比牛頓法更為有效。如今,最佳化軟體中包含了大量的擬牛頓算法用來解決無約束,約束,和大規模的最佳化問題。
3. 共軛梯度法(Conjugate Gradient)
共軛梯度法是介於最速下降法與牛頓法之間的一個方法,它僅需利用一階導數信息,但克服了最速下降法收斂慢的缺點,又避免了牛頓法需要存儲和計算Hesse矩陣並求逆的缺點,共軛梯度法不僅是解決大型線性方程組最有用的方法之一,也是解大型非線性最最佳化最有效的算法之一。在各種最佳化算法中,共軛梯度法是非常重要的一種。其優點是所需存儲量小,具有步收斂性,穩定性高,而且不需要任何外來參數。
4. 啟發式最佳化方法
啟發式方法指人在解決問題時所採取的一種根據經驗規則進行發現的方法。其特點是在解決問題時,利用過去的經驗,選擇已經行之有效的方法,而不是系統地、以確定的步驟去尋求答案。啟發式最佳化方法種類繁多,包括經典的模擬退火方法、遺傳算法、蟻群算法以及粒子群算法等等。
5. 拉格朗日乘數法的基本思想
作為一種最佳化算法,拉格朗日乘子法主要用於解決約束最佳化問題,它的基本思想就是通過引入拉格朗日乘子來將含有n個變數和k個約束條件的約束最佳化問題轉化為含有(n+k)個變數的無約束最佳化問題。拉格朗日乘子背後的數學意義是其為約束方程梯度線性組合中每個向量的係數。
將一個含有n個變數和k個約束條件的約束最佳化問題轉化為含有(n+k)個變數的無約束最佳化問題,拉格朗日乘數法從數學意義入手,通過引入拉格朗日乘子建立極值條件,對n個變數分別求偏導對應了n個方程,然後加上k個約束條件(對應k個拉格朗日乘子)一起構成包含了(n+k)變數的(n+k)個方程的方程組問題,這樣就能根據求方程組的方法對其進行求解。
數學模型
最最佳化問題的共同特點是:求滿足一定條件的變數x,x,…,x,使某函式f(x,x,…,x)取得最大值或者最小值。由於f(x,x,…,x)的最大問題可以轉化為-f(x,x,…,x)的最小問題,所以較多時候只討論最小問題。這裡的函式f(x,x,…,x)稱為目標函式或者評價函式;變數x,x,…,x稱為決策變數;需要滿足的條件稱為約束條件;用以構成約束條件的函式稱為約束函式。
問題分類
約束類型
1、無約束問題
求x=(x,x,…,x)使函式f(x)=f(x,x,…,x)達到最小值,記為min f(x)。
2、約束問題
根據約束函式的類型又可分為以下幾類:
(1)等式約束問題:求x=(x,x,…,x)使其在滿足l個等式約束條件h(x)=0,j=1,2,…,l的情況下,使函式f(x)=f(x,x,…,x)達到最小值,記為如圖公式
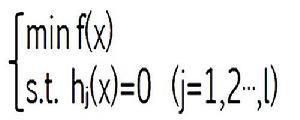 最最佳化
最最佳化 (2)不等式約束問題:求x=(x,x,…,x)使其在滿足m個不等式約束條件g(x)≥0,i=1,2,…,m 的情況下,使函式f(x)=f(x,x,…,x)達到最小值,記為如圖公式
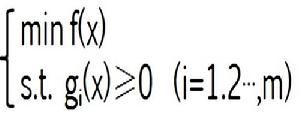 最最佳化
最最佳化 (3)混和約束問題或稱一般約束問題:求x=(x,x,…,x)使其在滿足m個不等式約束條件
g(x)≥0,i=1,2,…,m以及l個等式約束條件h(x)=0,j=1,2,…,l的情況下,使函式
f(x)=f(x,x,…,x)達到最小值,記為如圖公式
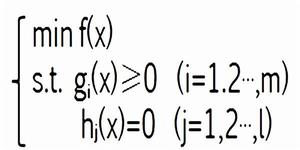 最最佳化
最最佳化 以上各問題中的函式f(x)=f(x,x,…,x)稱為目標函式,函式g(x)、h(x)稱為約束函式。滿足約束條件的點x構成的集合,稱為可行解集合,亦稱可行區或可行域。
目標約束函式
最最佳化問題也稱為規劃問題。
如果最最佳化問題的目標函式為f(x),約束條件為g(x)≥0,i=1,2,…,m則:
當f(x)和g(x)均為線性函式時,稱此最最佳化問題為線性規劃;
當f(x)和g(x)不全為線性函式時,稱此最最佳化問題為非線性規劃;
當f(x)為二次函式,而g(x)全為線性函式時,稱此最最佳化問題為二次規劃。
變數的類型
對於最最佳化問題,如果變數x=(x,x,…,x)的各分量只能取整數,則相應的最最佳化問題稱為整數規劃。
如果變數x=(x,x,…,x)的部分分量只能取整數,則相應的最最佳化問題稱為混合整數規劃。
如果變數x=(x,x,…,x)的各分量只能取0和1,則相應的最最佳化問題稱為0-1規劃。
最優解最優值
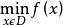 最最佳化
最最佳化 設最最佳化問題為(P) ,D={ x∣g(x)≥0,i=1,2,…,m}
定義1:
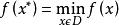 最最佳化
最最佳化 如果有x*∈D使得 ,即∃x*∈D,使得對∀x∈D有f(x)≥f(x*),則稱x* 為問題(P)的全局最優解,稱f(x*)為全局最優值。
在定義中,如果當∀x∈D且x≠x*時恆有f(x)>f(x*),則稱x*為問題(P)的嚴格全局最優解,稱f(x*)為嚴格全局最優值。
定義2:
如果有x*∈D及δ>0,使得當x∈D ∩ N(x*)時恆有f(x)≥f(x*),則稱x*為問題(P)的局部最優解,稱f(x*)為局部最優值。
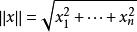 最最佳化
最最佳化 這裡的N(x*)={x∣‖x-x*‖
同樣,定義中,如果當x≠x* 時可將 “≥”改為 “>”,則稱x* 為問題(P)的嚴格局部最優解,稱f(x*)為嚴格局部最優值。

