簡介
正則表達式和非確定有限狀態自動機是形式語言的兩種不同的抽象表達方式。在諸如文本編輯器的高級“查找和替換”以及許多程式語言中，人們都習慣使用正則表達式來表示字元串的匹配模式。然而，當計算機執行匹配程式時，NFA卻是更加適合的一種格式。因此，Thompson構造法有著重要的套用價值，它實際上可以視作正則表達式到NFA的一個編譯器。而從理論角度上來說，該算法實際上是正則表達式和NFA等價性證明的一部分——事實上，這兩種表述形式本質上都對應著相同的語言，即正則語言。
在套用中，算法得到的NFA可以再次通過冪集構造和最小化的過程得到一個對應的最簡的確定有限狀態自動機（DFA），進而用於匹配正則表達式。但是有些情況下也會直接使用對應的NFA。
算法介紹
構造規則
算法通過遞歸地將一個正則表達式劃分成構成它的子表達式，在得到每個子表達式對應的NFA之後，根據子表達式之間的運算關係和一系列規則構造表達式自身對應的NFA。具體來說，這套構造規則如下所示：
遞歸終點
對於正則表達式為ε或者只由一個符號構成的情況，則無需繼續遞歸，對應的NFA可以直接由下列規則給出：
空表達式ε直接轉化為：
Thompson構造法字母表中的單個 符號 a直接轉化為：
Thompson構造法子表達式運算的構造規則
下面針對正則表達式的三種運算——並、連線和Kleene*閉包給出NFA的構造規則。設子表達式為s和t，則它們對應的NFA分別記作N(s)和N(t)。
兩個正則表達式的 並 s| t可以轉化為：
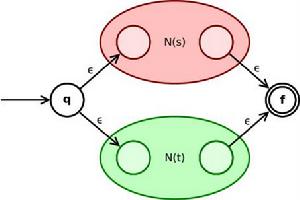Thompson構造法通過ε轉移， 狀態 q可以直接到達 N( s)或 N( t)的初態。而 N( s)或 N( t)原來的終態也可以通過ε轉移直接到達整個NFA的新終態。
連線表達式 s t可以轉化為：
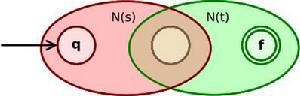Thompson構造法N( s)的初態成為新的NFA的初態。 原來 N( s)的終態成為 N( t)的初態。而原來 N( t)的終態成為新的NFA的終態。
Kleene*閉包 s可以轉化為：
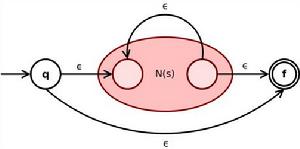Thompson構造法將新表達式的初態和終態以及夾在中間的子表達式的NFA N( s)連線起來的ε轉移使得可以選擇經過或者不經過子表達式。而從 N( s)的終態到初態的ε轉移使得 s可以重複任意多次。
•加括弧的表達式(s) 直接轉化為N(s) 自身即可。
非確定有限狀態自動機
在計算理論中， 非確定有限狀態自動機或 非確定有限自動機（NFA）是對每個狀態和輸入符號對可以有多個可能的下一個狀態的有限狀態自動機。這區別於確定有限狀態自動機（DFA），它的下一個可能狀態是唯一確定的。儘管DFA和NFA有不同的定義，在形式理論中可以證明它們是等價的；就是說，對於任何給定NFA，都可以構造一個等價的DFA，反之亦然：通過使用冪集構造。兩種類型的自動機只識別正則語言。非確定有限自動機有時被稱為有限類型的子移位（subshift）。非確定有限狀態自動機可推廣為機率自動機，它為每個狀態轉移指派機率。
非確定有限自動機是Michael O. Rabin和Dana Scott在1959年介入的，他們證明了它與確定自動機的等價性。
