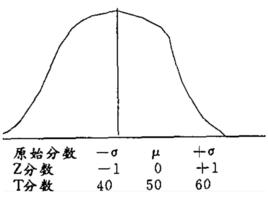
定義
T分數是原始分數的導出分數。把原始分數轉換成標準化分數為線性轉換,Z分數與原始分數的分布形狀相同,原始分數為常態分配,則Z分數也為常態分配。原始分數如果不是常態分配,如何使導出分數為常態分配呢?這時可先把原始分數轉換成百分等級,而後再把百分等級轉換成標準常態分配的z值,從而迫使導出分數z服從均數為0、標準差為1的常態分配,叫做正態化的標準分數。
求值公式
T分數的求值公式為:T=50+10Z,Z是一個數(X)與平均數(x)之差除以標準差(S)所得的商數。T分數的平均數是50,它的每一個標準差是10,所以,T分數為60等於平均數以上一個標準差的原始分數,T分數為70等於平均數以上兩個標準差的原始分數。
主要特點
T分數無實際單位,它的作用除表明原始分在分配中的位置外,還可比較不同分配的原始分數。如身高1.75米和體重70公斤,究竟哪一個在分配中所處的地位高是不能直接比較的。但求出T分數後就能進行比較。
使用條件
T分數是指T服從均數為50、標準差為10的常態分配。如果認為總體的原始分數為或近似為常態分配(這是編制試卷的要求),因為樣本含量小,抽樣誤差大,造成樣本的原始分數為偏態分布,則用T分數是合理的;若樣本的原始分數已近似常態分配,則用Z分數即可。如果總體的原始分數本身就為偏態分布(試卷編製得不好),則不宜用T分數,可用Z分數,最好用百分等級。