定理簡介
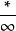 O'Stolz定理
O'Stolz定理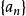 O'Stolz定理
O'Stolz定理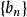 O'Stolz定理
O'Stolz定理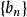 O'Stolz定理
O'Stolz定理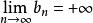 O'Stolz定理
O'Stolz定理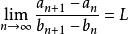 O'Stolz定理
O'Stolz定理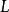 O'Stolz定理
O'Stolz定理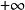 O'Stolz定理
O'Stolz定理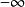 O'Stolz定理
O'Stolz定理( 型) 設數列 、 滿足:① 嚴格單調遞增 ② ③ (其中 可以為有限實數、 、 )
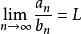 O'Stolz定理
O'Stolz定理則
這個是較常用的版本
 O'Stolz定理
O'Stolz定理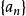 O'Stolz定理
O'Stolz定理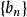 O'Stolz定理
O'Stolz定理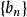 O'Stolz定理
O'Stolz定理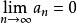 O'Stolz定理
O'Stolz定理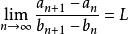 O'Stolz定理
O'Stolz定理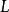 O'Stolz定理
O'Stolz定理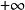 O'Stolz定理
O'Stolz定理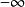 O'Stolz定理
O'Stolz定理( 型) 設數列 、 滿足:① 嚴格單調遞減且趨於零 ② ③ (其中 可以為有限實數、 、 )
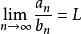 O'Stolz定理
O'Stolz定理則
證明過程
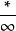 O'Stolz定理
O'Stolz定理一、 型
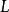 O'Stolz定理
O'Stolz定理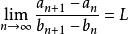 O'Stolz定理
O'Stolz定理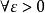 O'Stolz定理
O'Stolz定理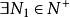 O'Stolz定理
O'Stolz定理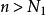 O'Stolz定理
O'Stolz定理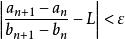 O'Stolz定理
O'Stolz定理(當 為有限實數時)由 , , ,當 時, , 即
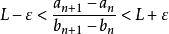 O'Stolz定理
O'Stolz定理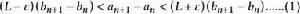 O'Stolz定理
O'Stolz定理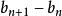 O'Stolz定理
O'Stolz定理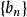 O'Stolz定理
O'Stolz定理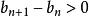 O'Stolz定理
O'Stolz定理(這裡可以把 乘到不等號另一邊是因為 嚴格單調遞增,所以 ,乘到不等號另一邊時不變號)
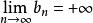 O'Stolz定理
O'Stolz定理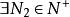 O'Stolz定理
O'Stolz定理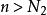 O'Stolz定理
O'Stolz定理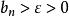 O'Stolz定理
O'Stolz定理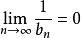 O'Stolz定理
O'Stolz定理又由 ,∴ ,當 時, (這裡是根據數列趨於正無窮大的定義),∴ (注一)
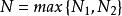 O'Stolz定理
O'Stolz定理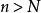 O'Stolz定理
O'Stolz定理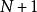 O'Stolz定理
O'Stolz定理 O'Stolz定理
O'Stolz定理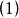 O'Stolz定理
O'Stolz定理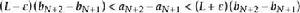 O'Stolz定理
O'Stolz定理取 ,當 時,從 到 對 式累加,有
 O'Stolz定理
O'Stolz定理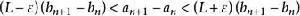 O'Stolz定理
O'Stolz定理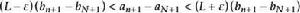 O'Stolz定理
O'Stolz定理累加得
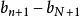 O'Stolz定理
O'Stolz定理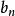 O'Stolz定理
O'Stolz定理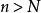 O'Stolz定理
O'Stolz定理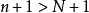 O'Stolz定理
O'Stolz定理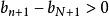 O'Stolz定理
O'Stolz定理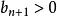 O'Stolz定理
O'Stolz定理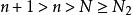 O'Stolz定理
O'Stolz定理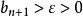 O'Stolz定理
O'Stolz定理同除 (還是因為 嚴格單調遞增, , , ),還注意到 ,因為 ,
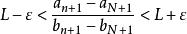 O'Stolz定理
O'Stolz定理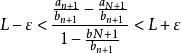 O'Stolz定理
O'Stolz定理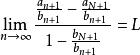 O'Stolz定理
O'Stolz定理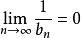 O'Stolz定理
O'Stolz定理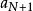 O'Stolz定理
O'Stolz定理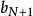 O'Stolz定理
O'Stolz定理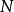 O'Stolz定理
O'Stolz定理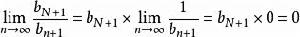 O'Stolz定理
O'Stolz定理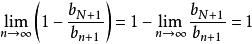 O'Stolz定理
O'Stolz定理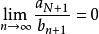 O'Stolz定理
O'Stolz定理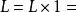 O'Stolz定理
O'Stolz定理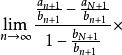 O'Stolz定理
O'Stolz定理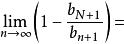 O'Stolz定理
O'Stolz定理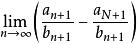 O'Stolz定理
O'Stolz定理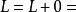 O'Stolz定理
O'Stolz定理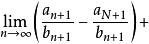 O'Stolz定理
O'Stolz定理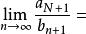 O'Stolz定理
O'Stolz定理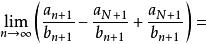 O'Stolz定理
O'Stolz定理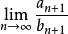 O'Stolz定理
O'Stolz定理即 ,由 ,且 、 是常數,因為 是確定的下標!由極限的四則運算法則, (注二), ,同理 ,再由極限的四則運算法則, , [1]
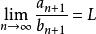 O'Stolz定理
O'Stolz定理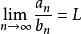 O'Stolz定理
O'Stolz定理即 ,
__________________________________________________________________________________________
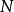 O'Stolz定理
O'Stolz定理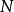 O'Stolz定理
O'Stolz定理為了方便初學者,這裡解釋一下以上的跳步。注意以下的註裡出現的符號與上面證明的符號是分開的!比 如注一的 與證明里的 不同啊,初學者不要搞混。
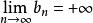 O'Stolz定理
O'Stolz定理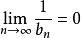 O'Stolz定理
O'Stolz定理注一:我們可以證明,若 ,則 ,
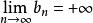 O'Stolz定理
O'Stolz定理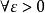 O'Stolz定理
O'Stolz定理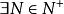 O'Stolz定理
O'Stolz定理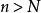 O'Stolz定理
O'Stolz定理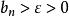 O'Stolz定理
O'Stolz定理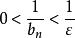 O'Stolz定理
O'Stolz定理 O'Stolz定理
O'Stolz定理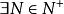 O'Stolz定理
O'Stolz定理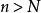 O'Stolz定理
O'Stolz定理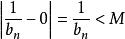 O'Stolz定理
O'Stolz定理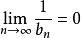 O'Stolz定理
O'Stolz定理證明:由 , , ,當 時, , ,∴ , ,當 時, ,即
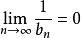 O'Stolz定理
O'Stolz定理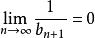 O'Stolz定理
O'Stolz定理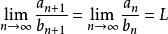 O'Stolz定理
O'Stolz定理注二:由注一, ,可推出 ,相當於去掉了第一項,然而極限是趨於無窮的行為,有沒有這一點對極限毫無影響,後面的 也是如此,當然這一點是可以證明的,這裡略去。可以看[2]的第4題的證明過程。
還有倒數第二段那裡一堆的使用極限四則運算法則,嚴謹性是達到了,為了初學者能正確掌握,但是看起來很繁瑣,其實這段裡面的一些步驟在已經學了數學分析的同學眼裡是已知的,無須寫出來的。所以如果你要在正式場合寫該定理的證明,以上證明中的 "因為 "後面的解釋說明和倒數第二段的繁雜過程可以刪減,按你的意願做相應簡化即可。
一個例子
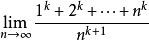 O'Stolz定理
O'Stolz定理例:求極限 (k為正整數)。
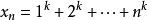 O'Stolz定理
O'Stolz定理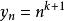 O'Stolz定理
O'Stolz定理解:令 ,
由O'Stolz定理
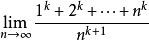 O'Stolz定理
O'Stolz定理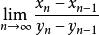 O'Stolz定理
O'Stolz定理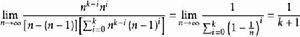 O'Stolz定理
O'Stolz定理= =
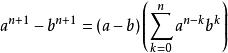 O'Stolz定理
O'Stolz定理註:

