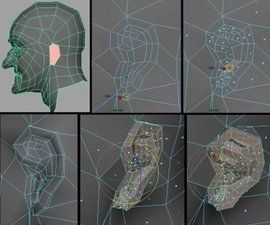
基本概述
NURBS是非均勻有理B樣條曲線（Non-Uniform Rational B-Splines）的縮寫，NURBS由Versprille在其博士學位論文中提出，1991年，國際標準化組織（ISO）頒布的工業產品數據交換標準STEP中，把NURBS作為定義工業產品幾何形狀的唯一數學方法。1992年，國際標準化組織又將NURBS納入到規定獨立於設備的互動圖形編程接口的國際標準PHIGS（程式設計師層次互動圖形系統）中，作為PHIGS Plus的擴充部分。Bezier、有理Bezier、均勻B樣條和非均勻B樣條都被統一到NURBS中。
NURBS曲線和NURBS曲面在傳統的製圖領域是不存在的，是為使用計算機進行3D建模而專門建立的。在3D建模的內部空間用曲線和曲面來表現輪廓和外形。它們是用數學表達式構建的，NURBS數學表達式是一種複合體。在這裡，只是簡要地介紹一下NURBS的概念，來幫助了解怎樣建立NURBS和NURBS物體為什麼會有這樣的表現。
nurbs
nurbs連續性
所有的曲線都有Degree(度數），又稱階數或次數。一條曲線的度數在表現所使用的等式裡面是最主要的指數。一個直線的等式度數是1，一個二次的等式度數是2.NURBS曲線表現是立方等式，度數是3.可以把度數設得很高，但通常不必要這樣做。雖然度數越高曲線越圓滑，但計算時間也越長。一般只要記住Degree(度數）值越高曲線越圓滑就可以了。
曲線也都有Continuity(連續性）。一條連續的曲線是不間斷的。連續性有不同的級別，一條曲線有一個角度或尖端，它的連續性是C0。一條曲線如果沒有尖端但曲率有改變，連續性是C1。如果一條曲線是連續的，曲率不改變，連續性是C2。
另外一種連續性的表示是幾何連續性，G0、G1、G2、G3 可以通過恰當的參數變換得到相應的C0、C1 、C2、C3。
一條曲線可以有較高的連續性，但對於計算機建模來說這三個級別已經夠了。通常眼睛不能區別C2連續性和更高的連續性之間的差別。
連續性和度數是有關係的。一個度數為3的等式能產生C2連續性曲線。NURBS造型通常不需要這么高度數的曲線。
一條不同片斷的NURBS曲線可以用不同級別的連續性。具體來說，在同樣的位置或非常靠近的地方放置一些可控點，會降低連續性的級別。兩個重疊的可控點會使曲率變尖銳。三個重疊的可控點會在曲線里建立一個有角度的尖角。附加一個或兩個可控點會在曲線的附近聯合它們的影響力。
從可控點中刪除一個離開它們，就增加了曲線的連續性的級別。在3DMAX里，Fuse(熔化）可控點會在曲線里建立一個假象的曲率或尖角。如果要恢復原狀，Unfuse(反熔化）那個點就可以了。
概念
在3DMAX里可以用點曲線和點曲面來建立模型。控制這些物體的點是被強制依附於曲線或曲面上的。它沒有黃色的虛線控制格和重量控制。這是一個比較簡單的界面，初學者可能更喜歡用。這並不是說高級用戶就用不上了，如果是那樣的話開發商就不會把它加到3DMAX中去了。可以用基礎點來構建一條曲線，然後構建從屬曲面。
可以使用按鈕來把點曲線或點曲面轉換成獨立的可控曲線或可控曲面。另一方面，儘量不要把可控曲線或曲面轉換成點曲線或曲面，因為這樣會有多種點的解決方案，會有難以遇料的結果。
容差
這裡先介紹一個容差的概念，以後將要用到。容差是指在3DMAX所使用的度量單位里的一個距離。如果連線的曲線間的間距大於這個值，3DMAX實際上是先建立一條融合曲線，然後再把三個部分連線在一起形成一條完整的曲線。如果間距小於這個值，則3DMAX不建立融合曲線。
先在兩條曲線間建立一條Blend(融合）曲線，然後把三條曲線連線在一起形成一條單個的曲線，這是一種比較好的方法，得到的結果與父曲線匹配得很好。
當有一個距離，但是它太小的時候會出現問題。在這種情況下，3DMAX要產生融合，但是因為那裡沒有足夠的空間給它，結果曲線會有一個環形在那裡。要避免這個環形，把Tolerance(容差）設定得比間距大就可以了。如果設定容差為0，3DMAX會為它選擇一個值。
起源
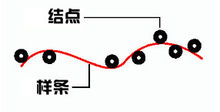樣條的最初定義樣條曲線是一類特殊的曲線，最初在計算機建模出現之前由船舶工業發展需求而創造並發展起來的。當時
海軍的設計師需要通過幾個點來畫一條光滑曲線。為此他們想出了一個簡單而有效的方法，就是將金屬重物（Weights）（這在後來的數學解釋上稱之為結點Knots）放置在控制點（Control Points）上，並使用薄金屬片繞過這些控制點自然彎曲得到光滑變化的形狀，他們把這個形狀稱之為樣條。
在物理上，樣條的形狀在結點處的影響最大並且沿著樣條遠離結點會逐漸減小，想要獲得對樣條某一區域更多的控制，只能在相應的區域增加更多的結點才行。
這種方案在數據交換的時候遇到了麻煩，因為要在不同的平台進行數據交換，人們必須用一種數學的方法來描述曲線的形狀，為此誕生了三次方程樣條。後來從多項式樣條引申出B樣條（基礎樣條），B樣條是低級別的多項式樣條的集合，為了適應更複雜的樣條數據交換，最後從B樣條又引申出了Nurbs樣條。
