簡介
在密碼學中， ElGamal加密算法是一個基於迪菲-赫爾曼密鑰交換的非對稱加密算法。它在1985年由塔希爾·蓋莫爾提出。GnuPG和PGP等很多密碼學系統中都套用到了ElGamal算法。
ElGamal加密算法可以定義在任何循環群G上。它的安全性取決於G上的離散對數難題。
算法
ElGamal加密算法由三部分組成：密鑰生成、加密和解密。
密鑰生成
密鑰生成的步驟如下：
（1）Alice利用生成元g產生一個q階循環群G的有效描述。該循環群需要滿足一定的安全性質。
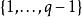ElGamal加密算法（2）Alice從中隨機選擇一個x。
ElGamal加密算法（3）Alice計算。
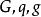ElGamal加密算法（4）Alice公開h以及的描述作為其 公鑰，並保留x作為其 私鑰。私鑰必須保密。
加密
使用Alice的公鑰(G,q,g,h)向她加密一條訊息 m的加密算法工作方式如下：
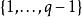ElGamal加密算法
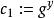ElGamal加密算法（1）Bob從隨機選擇一個y，然後計算。
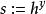ElGamal加密算法（2）Bob計算共享秘密。
（3）Bob把他要傳送的秘密訊息m映射為 G上的一個元素 m'。
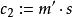ElGamal加密算法（4）Bob計算。
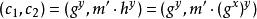ElGamal加密算法（5）Bob將密文傳送給Alice。
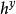ElGamal加密算法值得注意的是，如果一個人知道了m'，那么它很容易就能知道的值。因此對每一條信息都產生一個新的 y可以提高安全性。所以y也被稱作臨時密鑰。
解密
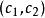ElGamal加密算法利用私鑰x對密文進行解密的算法工作方式如下：
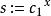ElGamal加密算法Alice計算共享秘密；
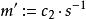ElGamal加密算法
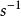ElGamal加密算法然後計算，並將其映射回明文m，其中是s在群G上的逆元。（例如：如果G是整數模n乘法群的一個子群，那么逆元就是模逆元）。
解密算法是能夠正確解密出明文的，因為
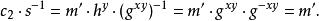ElGamal加密算法實際使用
ElGamal加密系統通常套用在混合加密系統中。例如：用對稱加密體制來加密訊息，然後利用ElGamal加密算法傳遞密鑰。這是因為在同等安全等級下，ElGamal加密算法作為一種非對稱密碼學系統，通常比對稱加密體制要慢。對稱加密算法的密鑰和要傳遞的訊息相比通常要短得多，所以相比之下使用ElGamal加密密鑰然後用對稱加密來加密任意長度的訊息，這樣要更快一些。
