簡介
efficient frontier:有效邊界
精要解釋
用來描述一項投資組合的風險與回報之間的關係,在以風險為橫軸,預期回報率為縱軸的坐標上顯示為一條曲線,所有落在這條曲線上的風險回報組合都是在一定風險或最低風險下可以獲得的最大回報。
投資套用
有效邊界是建立最優投資組合和證券估值最重要和有用的金融學理論。管理大規模資產的基金經理的工作重點就是如何將其投資組合的風險回報值落在有效邊界曲線上,那些還沒有達到或接近有效邊界的投資組合可以採取多元化投資在不增加風險的情況下提高回報率,或在降低風險的情況下不降低回報率。
為此馬克維茲依據以下幾個基本假設建立了有效邊界模型:
(l)投資者希望財富越多越好,且被投資效用為財富的增函式,但財富的邊際效用是遞減的。
(2)投資者事先知道投資報酬率分布為常態分布。
(3)投資者希望投資效用的期望值最大而該期望值是預期報酬率和風險的函式,因此影響投資決策的主要因素是預期報酬率和風險。
(4)投資者對風險是反感的,投資風險以預期報酬率的方差或標準差來表示。
(5)投資者理性的他遵循的原則是:在相同的預期報酬率下選擇風險小的證券,或者在相同的投資風險下選擇預期報酬率最大的證券。
(6)市場的有效性,即對本市場上一切信息都是已知者。
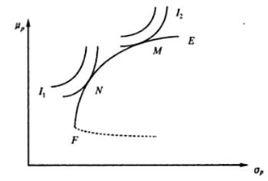
他們依據上述假設來尋有效的投資組合,在證券市場上可用於投資的投資證券種類繁多,因此投資者可以建立無數證券組合進行投資,那么何種證券組合是最有效的投資組合呢?馬克維茲認為,在用橫軸表示的投資組合的風險σ p、縱軸表示投資組合的預期報酬率μ p的坐標圖中,可以求得一條最有效率的投資組合邊界曲線EF。
圖:資產組合的有效邊界模型
在這條有效的邊界曲線上的所有點都是最有效的投資組合點,而在有效邊界以內各點的投資組合者是非有效的。由於在有效邊界上的每一種資產組合都是最有效的投資點,因此,投資者選擇哪一點組合取決於投資者偏好即投資差異曲線。圖中的 I1, I2分別代表兩種不同的投資偏好的無差異曲線,當投資者1選擇N點,能使該投資者獲得滿意的有效投資組合。而投資無差異曲線 I2與有效邊界EF相切於M點,則表明投資者2具有進攻型投資偏好,他願意以較高的風險換取更大投資報酬率。