介紹
數據加密有兩種方式，一種是對稱加密算法，另一種是公開密鑰加密算法。由於對稱加密算法加密和解密採用的是同一把密鑰，因此如何確保密鑰的安全傳遞成為難題。而公開密鑰解密算法相對較為安全，因此為確保密鑰的安全傳遞，有時候採用公開密鑰加密進行傳遞。但是成本也相對較高，Diffie-Hellman算法也能夠很好地實現密鑰的傳遞。
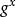Diffie-Hellman算法
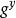Diffie-Hellman算法Diffie-Hellman算法，簡稱DH算法，由W.Diffie和M.E.Hellman在1976年公布的一種密鑰一致性算法，該算法是一種建立密鑰的方法，並非加密方法，但其產生的密鑰可用於加密、密鑰管理或任何其它的加密方式，這種密鑰交換技術的目的在於使兩個用戶間能安全地交換密鑰(KEY)以便用於今後的報文加密。該算法需要公開兩個參數：質數 n 和其原根 g，同時通信雙方 A 和 B 隨機選擇自己的私鑰 x 和 y，通過交換 mod n 和 mod n 後，它們就可以生成兩者之間的會話密鑰了。DH算法對公開密鑰密碼編碼學產生了深遠的影響。DH算法是一種確保共享KEY安全穿越網路的方法。
算法描述
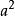Diffie-Hellman算法
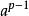Diffie-Hellman算法
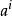Diffie-Hellman算法離散對數：定義素數p的原始根是能生成1-(p-1)之間所有數的一個數，設a為p的原始根，則：a mod p， mod p，…， mod p是各不相同的整數，且以某種排列方式組成了從1到p-1的所有整數。對於任意數b及素數p的原始根a，可以找到一個唯一的指數i，滿足：b= mod p，其中0≤i≤p-1，那么指數i 稱為b的以a為基數的模p的離散對數。
Diffie-Hellman算法的有效性依賴於計算離散對數的難度，其含義是：當已知大素數p和它的一個原根a後，對於給定的b，要計算出i 被認為是很困難的，而給定i 計算b卻相對容易。
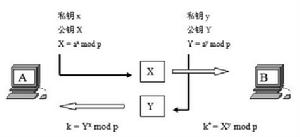圖1 Diffie-Hellman算法過程示意圖假設網路上有兩個用戶A和B，彼此之間協商共同的密碼，算法過程如圖1所示。
假設交換密鑰的值為k。
(1)A和B事先約好大素數p和它的原始根a；
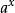Diffie-Hellman算法(2)A隨機產生一個數x，計算X= mod p，然後把X發給B；
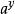Diffie-Hellman算法(3)B隨機產生一個數y，計算Y= mod p，然後把Y發給A；
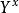Diffie-Hellman算法(4)A計算k= mod p；
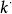Diffie-Hellman算法
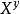Diffie-Hellman算法(5)B計算 = mod p。
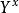Diffie-Hellman算法
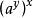Diffie-Hellman算法
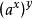Diffie-Hellman算法 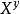Diffie-Hellman算法 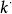Diffie-Hellman算法 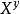Diffie-Hellman算法 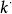Diffie-Hellman算法因為：k= mod p= mod p= mod p= mod p； = mod p；所以k= 。
不安全網路上的竊聽者只能得到a、p、X、Y，除非能計算離散對數x和y，否則將無法得到密鑰k，但對於大素數p，計算離散對數是十分困難的，因此k為用戶A和B獨立計算出的密鑰。
算法實現
編程思路：輸入一個素數和它的一個原始根，生成小於此素數的一個隨機數，計算出用戶的公鑰，保存信息。然後再輸入對方的公鑰，計算出雙方的會話密鑰。核心代碼如圖2所示，程式在Windows XP作業系統下，Visual C++ 2012環境中編譯通過。
圖2 Diffie-Hellman算法的C++編程核心代碼計算方法
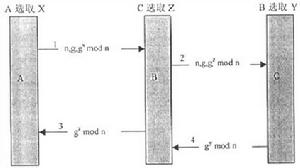圖3 Diffie-Hellman算法的中間人攻擊 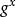Diffie-Hellman算法 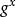Diffie-Hellman算法
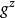Diffie-Hellman算法儘管Diffie-Hellman算法十分巧妙，但它也存在一個問題：當B得到一個三元組(n，g， mod n)時，他怎么知道這是來自於A而不是網路攻擊者C呢?他無法知道。不幸的是，C可以利用這一點來欺騙A和B，如圖3所示。當A和B分別選擇X和Y時，C也選擇了自己的隨機數Z並計算Z= mod n。
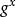Diffie-Hellman算法(1)A傳送X= mod n給B，C截獲了這條訊息。
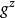Diffie-Hellman算法(2)C傳送Z= mod n給B，代替A的訊息。
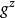Diffie-Hellman算法(3)C傳送Z= mod n給A，代替B的訊息。
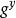Diffie-Hellman算法(4)B傳送Y= mod n給A，C截獲了這條訊息並保存起來。
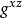Diffie-Hellman算法
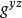Diffie-Hellman算法現在每個人都進行取模計算。A計算出的密鑰是 mod n，C也是(從發往A的訊息可知)。B計算出的密鑰是 mod n，C也是(從發往B的訊息可知)。A認為她與B通話，因此她建立了一個會話密鑰(和C)，B也是一樣。A傳送的所有加密信息都被C截獲，存儲。他還可以任意修改信息，然後可以傳送給B。在另一方向也是這樣，C了解一切並能夠任意修改訊息，而A和B卻被假象所迷惑，他們以為雙方已擁有了一條安全的信息通道。即使事後A和B知道有人攻擊，但也無法確定是誰，因為網路上的任何人都可以發起中間人攻擊。
利弊分析
由於密鑰交換過程中，交換值只有a、p、X、Y有可能被竊取，因此即使第三方竊取了a、p、X、Y的值，仍然很難推到出k的值來，尤其是當a、p、X、Y取值較大的時候更是難以破解出k的值來。從而增加了密鑰的安全性，因為從頭到尾密鑰沒有出現在網路上。但是問題是，如果a、p、X、Y取值較大也增加了彼此雙方計算餘數的難度，mod運算結果將會出現誤差，因此需要專門編程進行大整數取余運算來實現或用專門的邏輯計算電路來實現。
同公開密鑰加密算法相比，對於密鑰的管理相對複雜一些，因為需要進行相關計算。而公開密鑰加密算法直接傳遞的就是加密密鑰，直接解密就可以了，但是一旦私有密鑰丟失也面臨巨大的泄密風險。因此為確保數據安全，應加強私有密鑰的管理，防止私有密鑰泄露造成不必要的損失。
