內容
CS變值方法CS變值方法是以礦產儲量計算為例首次揭示了數學上的變值方法，其重點是變值方法。而變值方法的對應學科應叫變值數學，它是以同名坐標單位處處可變的各種變值坐標系及其對應函式（即各種變值函式）為基礎，並通過各種變值運算從巨觀和微觀方面定量研究各種數與形的動態特徵和變化規律。其中，同名坐標單位處處可變是變值方法的核心，其定量表達叫坐標係數或變值係數，變值係數可為首項為一非0常數的任意初等函式，而各種變值坐標系、變值函式和變值運算都要有變值係數的適當參與，且當變值係數恆為常數1時便與常規坐標系、常規函式和常規運算完全相同。因此，前者是對後者的重大擴展（如同實數是對有理數的合理擴展一樣）。
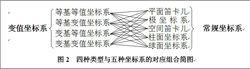CS變值方法
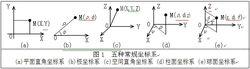
CS變值方法其中，變值坐標系可有等基等值（屬常規坐標系）、等基變值、變基等值和變基變值四種類型，目前較為常用的變值坐標係為箱變坐標系。上述四種類型與常規的五種坐標系（圖1）按圖2方式可構成20種 組合種類，可滿足各種空間類型的對應需求。與上述變值坐標系種類相對應可有各種變值函式，各種變值函式有一個共同的基本性質，即 變值 函式的自變數與基距同時擴大或縮小非零倍數，其值不變。此即 變值 函式的基本性質。這一性質的本質與分數的基本性質完全相同，由此便可對變值函式進行變基運算、通基變換及其它各種有關運算。現已探討的有關變值運算主要有1—3元的四則運算、不同空間的合併運算、積分運算，合併積分運算等。
套用
在套用方面，該法首先用於礦產資源儲量估算（即 CS儲量積分法），已首次解決了對各種圈礦模型的“精確快捷定位”計算的世界難題。同時，作為一種新型數學方法，該法不僅適用於現代數學的所有套用領域，還可使許多現有數學難題不再疑難，諸如各種巨觀和微觀的扭面問題、非線性不均勻扭曲及各種動態膨脹收縮空間等問題的精確表達和有關精確運算等。隨著該法的不斷完善和進一步推廣套用，將會推動現代數學及其相關學科的重大突破或變革。
