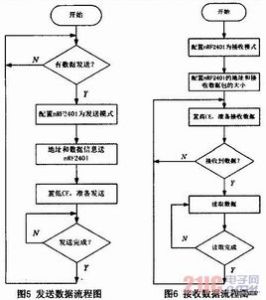
生成方法
 CRC校驗
CRC校驗藉助於模2除法則,其餘數為校驗欄位。
例如:信息欄位代碼為:1011001;對應m(x)=x6+x4+x3+1
假設生成多項式為:g(x)=x4+x3+1;則對應g(x)的代碼為:11001
x4m(x)=x10+x8+x7+x4對應的代碼記為:10110010000;
採用模2除法則:得餘數為:1010(即校驗欄位為:1010)
傳送方:發出的傳輸欄位為:10110011010
信息欄位校驗欄位
接收方:使用相同的生成碼進行校驗:接收到的欄位/生成碼(二進制除法)
如果能夠除盡,則正確,
給出餘數(1010)的計算步驟:
除法沒有數學上的含義,而是採用計算機的模二除法,即除數和被除數做異或運算。進行異或運算時除數和被除數最高位對齊,按位異或。
10110010000
^11001
--------------------------
01111010000
1111010000
^11001
-------------------------
0011110000
11110000
^11001
--------------------------
00111000
111000
^11001
-------------------
001010
則四位CRC校驗碼就為:1010。
利用CRC進行檢錯的過程可簡單描述為:在傳送端根據要傳送的k位二進制碼序列,以一定的規則產生一個校驗用的r位監督碼(CRC碼),附在原始信息後邊,構成一個新的二進制碼序列數共k+r位,然後傳送出去。在接收端,根據信息碼和CRC碼之間所遵循的規則進行檢驗,以確定傳送中是否出錯。這個規則,在差錯控制理論中稱為“生成多項式”。
算法
在代數編碼理論中,將一個碼組表示為一個多項式,碼組中各碼元當作多項式的係數。例如 1100101 表示為1·x+1·x+0·x+0·x+1·x+0·x+1,即 x+x+x+1。
設編碼前的原始信息多項式為P(x),P(x)的最高冪次加1等於k;生成多項式為G(x),G(x)的最高冪次等於r;CRC多項式為R(x);編碼後的帶CRC的信息多項式為T(x)。
傳送方編碼方法:將P(x)乘以xr(即對應的二進制碼序列左移r位),再除以G(x),所得餘式即為R(x)。用公式表示為T(x)=xrP(x)+R(x)
接收方解碼方法:將T(x)除以G(x),得到一個數,如果這個餘數為0,則說明傳輸中無錯誤發生,否則說明傳輸有誤。
舉例來說,設信息編碼為1100,生成多項式為1011,即P(x)=x3+x2,G(x)=x3+x+1,計算CRC的過程為
xrP(x) =x3(x3+x2) = x6+x5 G(x)= x3+x+1 即 R(x)=x。注意到G(x)最高冪次r=3,得出CRC為010。
如果用豎式除法(計算機的模二,計算過程為
1110 ------- 1011 /1100000 (1100左移3位) 1011 ---- 1110 1011 ----- 1010 1011 ----- 0010 0000 ---- 010 因此,T(x)=(x6+x5)+(x)=x6+x5+x, 即 1100000+010=1100010
如果傳輸無誤,
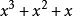 CRC校驗
CRC校驗T(x)= (x6+x5+x)/G(x) = , G(x)= 無餘式。回頭看一下上面的豎式除法,如果被除數是1100010,顯然在商第三個1時,就能除盡。
上述推算過程,有助於我們理解CRC的概念。但直接編程來實現上面的算法,不僅繁瑣,效率也不高。實際上在工程中不會直接這樣去計算和驗證CRC。
下表中列出了一些見於標準的CRC資料:
| 名稱 | 生成多項式 | 簡記式* | 套用舉例 |
| CRC-4 | x4+x+1 | 3 | ITU G.704 |
| CRC-8 | x8+x5+x4+1 | 31 | DS18B20 |
| CRC-12 | x12+x11+x3+x+1 | 5E | |
| CRC-16 | x16+x15+x2+1 | 8005 | IBM SDLC |
| CRC-ITU** | x16+x12+x5+1 | 1021 | ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCS,ZigBee |
| CRC-32 | x32+x26+x23+...+x2+x+1 | 04C11DB7 | ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCS |
| CRC-32c | x32+x28+x27+...+x8+x6+1 | 1EDC6F41 | SCTP |
* 生成多項式的最高冪次項係數是固定的1,故在簡記式中,將最高的1統一去掉了,如04C11DB7實際上是104C11DB7。 ** 前稱CRC-CCITT。ITU的前身是CCITT。
備註:
(1)生成多項式是標準規定的
(2)CRC校驗碼是基於將位串看作是係數為0或1的多項式,一個k位的數據流可以看作是關於x的從k-1階到0階的k-1次多項式的係數序列。採用此編碼,傳送方和接收方必須事先商定一個生成多項式G(x),其高位和低位必須是1。要計算m位的幀M(x)的校驗和,基本思想是將校驗和加在幀的末尾,使這個帶校驗和的幀的多項式能被G(x)除盡。當接收方收到加有校驗和的幀時,用G(x)去除它,如果有餘數,則CRC校驗錯誤,只有沒有餘數的校驗才是正確的。
(3) 名稱 生成多項式 簡記式* 標準引用
CRC-4 x4+x+1 3 ITU G.704
CRC-8 x8+x5+x4+1 0x31
CRC-8 x8+x2+x1+1 0x07
CRC-8 x8+x6+x4+x3+x2+x1 0x5E
CRC-12 x12+x11+x3+x+1 80F
CRC-16 x16+x15+x2+1 8005 IBM SDLC
CRC16-CCITT x16+x12+x5+1 1021 ISO HDLC,ITU X.25,V.34/V.41/V.42, PPP-FCS
CRC-32 x32+x26+x23+...+x2+x+1 04C11DB7 ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCS
CRC-32c x32+x28+x27+...+x8+x6+1 1EDC6F41 SCTP。
校驗電路實現
以下以CRC8x8+x5+x4+1為例說明,其它可以以此類推
生成算法
一個簡單的RTL解釋,是上文“生成方法”的Verilog描述
module CRC8(EN,data,crc);
parameter WIDTH=12;
input EN;
output[7:0]crc;
input[WIDTH-1:0]data;
reg[7:0]crc;
wire[7:0]poly=8'h31;
//x8+x5+x4+1-->0x131,ignore MSB
reg[WIDTH-1+8:0]crc_reg;
integer len;
always@(EN)
begin
if(!EN)
begin
crc=8'h00;
crc_reg={data,8'h00};
end
else
begin
for(len=WIDTH;len>0;len=len-1'b1)
begin
if(crc_reg[WIDTH-1+8])
begin
crc_reg=crc_reg<<1'b1;
crc_reg[WIDTH-1+8:WIDTH]=crc_reg[WIDTH-1+8:WIDTH]^poly;
end
else
crc_reg=crc_reg<<1'b1;
end
crc=crc_reg[WIDTH-1+8:WIDTH];
$display("Convertion done! CRC is: 0x%2x",crc);
end
end
endmodule
檢測電路
 CRC-8的電路框圖
CRC-8的電路框圖module crc(dataout,datain,clk,rst);
input clk,rst,datain;
output dataout;
DFF a1(clk,dataout,Q7,rst),
a2(clk,Q7,Q6,rst),
a3(clk,Q6,Q5,rst),
a4(clk,Q5,Q4,rst);
xor a5(temp5,Q4,dataout);
DFF a6(clk,temp5,Q3,rst);
xor a7(temp4,Q3,dataout);
DFF a8(clk,temp4,Q2,rst),
a9(clk,Q2,Q1,rst),
a10(clk,Q1,Q0,rst);
xor a11(dataout,Q0,datain);
endmodule
////////////////////////////////////////
module DFF(clk,D,Q,rst);
input clk,D,rst;
output Q;
 Verilog簡單測試
Verilog簡單測試reg Q;
always@(posedge clk or posedge rst)
begin
if(rst)
Q<=0;
else
Q<=D;
end
endmodule