定義
一個語言 L在 BPP裡面，若且唯若這語言存在一個機率圖靈機 M，另
•M對任何輸入均在多項式時間後停止
•對任何字串x在L之內, 對M輸入x之後，M輸出 1 的機率大於或者等於 2/3
•對任何字串x不在L之內, 對M輸入x之後，M輸出 1 的機率小於或者等於 1/3
另外， BPP可以僅以決定性圖靈機定義。一個語言 L是在 BPP裡面若且唯若存在一個多項式 p和一個決定性圖靈機 M，滿足
•M對任何輸入均操作多項式時間之內
•對任何字串x在L之內, 對長度為p(|x|)的任意字串y，滿足M(x,y)= 1 這條件的機率超過或等於2/3
•對任何字串x不在L之內, 對長度為p(|x|)的任意字串y，滿足M(x,y)= 1 這條件的機率小於或等於1/3
與其他複雜度類別的關係
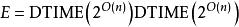BPP複雜度
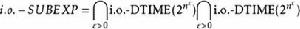BPP複雜度
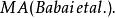BPP複雜度已知BPP在取補集之下有封閉性; 換句話說,BPP=Co-BPP。BPP是否是NP的子集仍舊是一個公開的問題。 另外NP是否是BPP的子集也是個公開的問題; 如果是的話，則NP=RP並且PH{\displaystyle \subseteq }BPP([2]) (大多數人認為不會，因為這代表對一些很難的NP-完全問題有著實際的解法)。現在已知RP是BPP的子集，並且BPP是PP的子集。 尚不清楚這兩個是否為嚴格子集。BPP包含在PH裡面。因此之故，P=NP代表BPP=P，因為PH在這時會變成P。 存在特定夠強的偽亂數產生器是這領域裡面大多數專家的猜想。這個猜想代表隨機性並不給予多項式計算更多的能力：換句話說，P=RP=BPP。注意一般的產生器並不足以表示出結果；使用典型的亂數產生器實做的任何機率算法，與亂數的種子無關，對某一些特定的輸入會一直給出錯誤的答案(即使這一些輸入可能很稀少)。我們也可得到P=BPP，若指數時間等級等同於 (Babai et al.),或者若E有指數的電路複雜性(Impagliazzo and Wigderson)。 又BPP包含在 裡面，若EXPTIME並不等同於
一個Monte Carlo算法是一個"差不多正確"的隨機算法。 與跟它很像的拉斯維加斯算法比較，後者則是一個永遠正確的隨機算法，不過隨機性在於有可能會回傳推算失敗。多項式時間之內的拉斯維加斯算法可以用來定義ZPP這個複雜度類。
BPP包含在P/poly裡面， 根據Adleman的理論，BPP是包含於P (複雜度)裡面的。; 的確，根據這個事實證明的結果，每一個BPP的算法，只要輸入是有限長度的話，我們可以藉由一個決定性算法去找足夠長的隨機字串來消除BPP的隨機特性。不過問題在於找到這個字串可能是很花費時間的事情。
其他特性
有很長一段時間, 一個非常有名的題目已知是BPP但不確定是否是P，是質數檢測，也就是求一個給定的數字是否是質數。 然而,在2002年的論文PRIMES is in P,Manindra Agrawal與他的學生Neeraj Kayal和Nitin Saxena為了這個問題找到了一決定性，多項式時間的算法，因而證實這個問題是在P裡面。
一個很重要的範例問題已知在BPP內 (事實上在co-RP內)，但不知道是否在P之內。這問題是等同多項式檢定, 這問題在於決定一個多項式是否完全等同於一個零多項式。 換句話說，是否存在任何變數數值的組合令這個多項式的結果不為零？ 這題目應均勻且隨意的從一個至少d個值的有限集合取變數的值來達到有限機率的錯誤(d代表多項式的總次數)。
BPP是低對應於自己 , 代表一個能在常數時間內解決BPP問題的BPP機器 (一個BPP啟示圖靈機) ，他的運算能力並不因此比沒有這能力的機器更強(或說，兩個不同機器定義出來的問題種類維持不變)。
BPP這個語言集合是以一個普通的圖靈機加上一個亂數的來源來定義。 相對應的量子計算機語言集合則是BQP。
任何在BPP裡面的語言可以被多項式大小的布林線路來決定。
