重要性
AKS最關鍵的重要性在於它是第一個被發表的 一般的、 多項式的、 確定性的和 無仰賴的素數判定算法。先前的算法至多達到了其中三點，但從未達到全部四個。
•AKS算法可以被用於檢測任何一般的給定數字是否為素數。很多已知的高速判定算法只適用於滿足特定條件的素數。例如，盧卡斯-萊默檢驗法僅對梅森素數適用，而Pépin測試僅對費馬數適用。
•算法的最長運行時間可以被表為一個目標數字長度的多項式。ECPP和APR能夠判斷一個給定數字是否為素數，但無法對所有輸入給出多項式時間範圍。
•算法可以確定性地判斷一個給定數字是否為素數。隨機測試算法，例如米勒-拉賓檢驗和Baillie–PSW，可以在多項式時間內對給定數字進行校驗，但只能給出機率性的結果。
•AKS算法並未“仰賴”任何未證明猜想。一個反例是確定性米勒檢驗：該算法可以在多項式時間內對所有輸入給出確定性結果，但其正確性卻基於尚未被證明的廣義黎曼猜想。
概念
AKS 素數測試主要是基於以下定理：整數 n(≥ 2)是素數，若且唯若
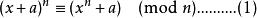AKS素數測試這個同餘多項式對所有與 n互素的整數 a均成立。 這個定理是費馬小定理的一般化，並且可以簡單的使用二項式定理跟二項式係數的這個特徵:
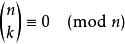AKS素數測試，對任何 0<k<n ，若且唯若 n是素數
來證明出此定理。
雖然說關係式 (1) 基本上構成了整個素數測試，但是驗證花費的時間卻是指數時間。因此，為了減少計算複雜度, AKS改為使用以下的同餘多項式：
AKS素數測試這個多項式與存在多項式 f與 g，令:
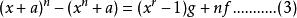AKS素數測試意義是等同的。
這個同餘式可以在多項式時間之內檢查完畢。這裡我們要注意所有的素數必定滿足此條件式 (令 g=0 則 (3) 等於 (1)，因此符合 n必定是素數)。 然而，有一些合數也會滿足這個條件式。有關AKS正確性的證明包含了推導出存在一個夠小的 r以及一個夠小的整數集合 A，令如果此同餘式對所有 A裡面的整數都滿足，則 n必定為素數。
歷史以及運算時間
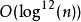AKS素數測試
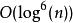AKS素數測試在上文引用的論文的第一版本中，作者們證明了算法的漸近時間為。換言之，算法使用少於 n的二進制數字長度的十二次方。但是，論文證明的時間上界卻過於寬鬆；事實上，一個被普遍相信的關於索菲熱爾曼素數分布的假設如果為真，則會立即將最壞情況減至。
在這一發現後的幾個月中，新的變體陸續出現（Lenstra 2002, Pomerance 2002, Berrizbeitia 2003, Cheng 2003, Bernstein 2003a/b, Lenstra和Pomerance 2003）並依次提高了算法的速度（以改進幅度為序）。由於這些變體的出現，Crandall和Papadopoulos在其科學論文“AKS-類素數測試的實現”（2003年三月發表）中將其稱為算法的“AKS-類”。
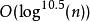AKS素數測試
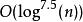AKS素數測試出於對這些變體和其他回復的回應，論文“素數屬於P”稍後被進行了更新，新版本包括了一個AKS算法的正規公式化表述和其正確性證明。（這一版本在數學年刊上發表。）雖然基本思想沒有變化， r卻被採用了新方法進行選擇，而正確性證明也變得更加緊緻有序。與舊證明依賴於許多不同的方法不同，新版本幾乎只依賴於有限域上的分圓多項式的特徵。新版本同時也最佳化了時間複雜度的邊界到。通過篩法獲得的其他結果可以將其進一步簡化到。
在2005年，Carl Pomerance和H. W. Lenstra, Jr.展示了一個AKS的變體，可以在O(log( n))次操作內完成測試（ n是被測試數）。對於原算法的O(log( n))邊界而言，這是一個顯著的改進。
算法
整個算法的操作如下：
輸入：整數 n>1；
若存在整數 a>0 且 b>1 ，令 n= a；則輸出 合數；
找出最小的 r令 ord( n)>log( n)；
若 對某些 a≤ r，1<gcd( a, n)< n，輸出 合數。(gcd是指最大公約數)。
若 n≤ r, 輸出 素數。
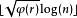AKS素數測試對 a=1 到的所有數，
如果 ( X+ a)≠ X+ a(mod X− 1, n), 輸出 合數。
輸出 素數。
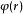AKS素數測試這裡的 ord( n)是 nmod r的階。 另外，這裡的 log代表以二為底的對數，則是 r的歐拉函式。
下面說明若 n是個素數，那么算法總是會返回 素數：由於 n是素數，步驟1和3永遠不會返回 合數。步驟5也不會返回 合數，因為(2)對所有素數 n為真。因此，算法一定會在步驟4或6返回 素數。
對應地，如果 n是合數，那么算法一定返回 合數：如果算法返回 素數，那么則一定是從步驟4或6返回。對於前者，因為 n≤ r， n必然有因子 a≤ r符合1 < gcd( a, n) < n，因此會返回 合數。剩餘的可能性就是步驟6，在文章中，這種情況被證明不會發生，因為在步驟5中檢驗的多個等式可以確保輸出一定是 合數。
