ABEL[十九世紀挪威數學家]

尼爾斯·亨利克·阿貝爾（1802年8月5日－1829年4月6日），挪威數學家，在很多數學領域做出了開創性的工作。他最著名的一個結果是首次完整給出了高於四次的一般代數方程沒有一般形式的代數解的證明。這個問題是他那時最著名的未解決問題之一，懸疑達250多年。他也是橢圓函式領域的開拓者，阿貝爾函式的發現者。儘管阿貝爾成就極高，卻在生前沒有得到認可，他的生活非常貧困，去世時只有27歲。

清貧少年

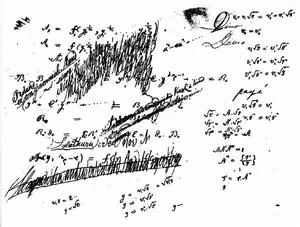阿貝爾的手稿之一。

阿貝爾（Niels Henrik Abel，1802年8月5日─1829年 4月 6日）是十九世紀挪威出現的最偉大數學家。他的父親是挪威克里斯蒂安桑（Kristiansand）主教區芬杜（Findö）小村莊的牧師，全家生活在窮困之中。在1815年，當他進入了奧斯陸的一所天主教學校讀書，他的數學才華便顯露出來。經他的老師霍爾姆伯（Holmboë）的引導下，他學習了不少當時的名數學家的著作，包括：牛頓（Newton）、歐拉（Euler）、拉格朗日（Lagrange）及高斯（Gauss）等。他不單了解他們的理論，而且可以找出他們一些微小的漏洞。

1820年，阿貝爾的父親去世，照顧全家七口的重擔突然交到他的肩上。雖然如此，1821年阿貝爾透過霍姆彪的補助，仍可進入奧斯陸的克里斯蒂安尼亞大學（University of Christinania），即奧斯陸大學（Universitetet i Oslo）就讀，於1822年獲大學預頒學位，並由霍姆彪的資助下繼續學業。在學校里，他幾乎全是自學，同時花大量時間作研究。

隱沒天才

ABEL[十九世紀挪威數學家]

1823年當阿貝爾的第一篇論文發表後，他的朋友便力請挪威政府資助他到德國及法國進修。當等待政府回復時，在1824年他發表了他的《一元五次方程沒有代數一般解》的論文，渴望為他帶來肯定地位。他把論文寄了給當時有名的數學家高斯，可惜高斯錯過了這篇論文，也不知道這個著名的代數難題已被解破。 1825-26年的冬季，他遠赴柏林，並認識了克列爾（Crelle）。克列爾是個土木工程師，而且對數學很有熱誠，他跟阿貝爾成為很要好的朋友。1826年，在阿貝爾的鼓勵下，克列爾創立了一份純數學和套用數學雜誌（Journal für die reine und angewandte Mathematik），該雜誌的第一期便刊登了阿貝爾在五次方程的工作成果，另外還有方程理論、泛函方程及理論力學等的論文。在柏林，新的數學嚮導使他繼續獨立地進行研究工作，後來阿貝爾更到了歐洲不同的地方。

1826年夏天，他在巴黎造訪了當時最頂尖的數學家，並且完成了一份有關超越函式的研究報告。這些工作展示出一個代數函式理論，現稱為阿貝爾定理，而這定理也是後期阿貝爾積分及阿貝爾函式的理論基礎。他在巴黎被冷落對待，他曾經把他的研究報告寄去科學學院，望可得到好評，但他的努力也是徒然。他在離開巴黎前染頑疾，最初只以為只是感冒，後來才知道是肺結核病。

ABEL[十九世紀挪威數學家]

他輾轉回到挪威，但欠下不少錢債。他只好靠教書及收取大學的微薄津貼為生。在1828年，他找到一份代課教師之職來維持生計。但他的窮困及病況並沒有減低他對數學的熱誠，他在這段期間寫了大量的論文，主要是方程理論及橢圓函式，也就是有關阿貝爾方程和阿貝爾群的理論。他比雅可比（Jacobi）更快完全了橢圓函式的理論。此時，阿貝爾的名聲經已響遍所有的數學中心，各方面的人也希望為他找到一個適當的教授席位，當中克列爾便希望為他在柏林找得一個教授席位。

在1828年冬天，阿貝爾的病逐漸嚴重起來。在他聖誕節去芬羅蘭（Froland）探他的未婚妻克萊利·肯姆普（Crelly Kemp）期間，病情便更惡化。到1829年1月時，他已知自己壽命不長，出血的症狀已無法否認。直至1829年4月6日凌晨，阿貝爾去世了，他的未婚妻堅持不要他人之助照顧阿貝爾，“單獨占有這最後的時刻”。

阿貝爾的未婚妻。

阿貝爾去世後，他的老師霍爾姆伯於1839年為他出版了文集。

遲到榮譽

直到阿貝爾去世前不久，人們才認識到他的價值。1828年，四名法國科學院院士上書給挪威國王，請他為阿貝爾提供合適的科學研究位置，勒讓德也在科學院會議上對阿貝爾大加稱讚。在阿貝爾死後兩天，克列爾寫信說為阿貝爾成功爭取於柏林大學（Freie Universität Berlin）當數學教授，可惜已經太遲，一代天才數學家已經在收到這訊息前去世了。此後榮譽和褒獎接踵而來，1830年他和卡爾·雅可比共同獲得法國科學院大獎。

阿貝爾的簽名。

阿貝爾在數學方面的成就是多方面的。除了五次方程之外，他還研究了更廣的一類代數方程，後人發現這是具有交換的伽羅瓦群的方程。為了紀念他，後人稱交換群為阿貝爾群。阿貝爾還研究過無窮級數，得到了一些判別準則以及關於冪級數求和的定理。這些工作使他成為分析學嚴格化的推動者。

阿貝爾和雅可比是公認的橢圓函式論的奠基者。阿貝爾發現了橢圓函式的加法定理、雙周期性、並引進了橢圓積分的反演。他研究了形如的積分(現稱阿貝爾積分)， 其中R(x，y)是x和y的有理函式，且存在二元多項式ƒ，使ƒ(x，y)=0。他還證明了關於上述積分之和的定理，現稱阿貝爾定理，它斷言：若干個這種積分之和可以用g個這種積分之和加上一些代數的與對數的項表示出來，其中g只依賴於ƒ，就是ƒ的虧格。阿貝爾這一系列工作為橢圓函式論的研究開拓了道路，並深刻地影響著其他數學分支。埃爾米特曾說：阿貝爾留下的思想可供數學家們工作150年。

科學院秘書傅立葉讀了論文的引言，然後委託勒讓得和柯西負責審查。柯西把稿件帶回家中，究竟放在什麼地方，竟記不起來了。直到兩年以後阿貝爾已經去世，失蹤的論文原稿才重新找到，而論文的正式發表，則遷延了12年之久。