簡介
5r覆蓋引理是R 中閉球族的一種覆蓋定理。
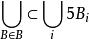5r覆蓋引理該引理斷言：設ℬ為R 中有界區域內的閉球族，則存在可列或有限個彼此不相交的子球族{B}，使得其中5B表示與B同心，半徑為B5倍的球。
覆蓋
覆蓋是數學術語，設Ф是拓撲空間X的子集族，稱Ф是X的一個覆蓋，如果對任意x∈X，x至少包含在Ф的一個成員之中。
維塔利覆蓋引理
數學上，維塔利(Vitali)覆蓋引理是一個組合幾何的結果，用於實分析中。這引理說給出一族球，可以從中找到互不相交的球，將這些球半徑增加一定倍後，就能把其他的球都覆蓋住。
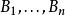5r覆蓋引理
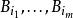5r覆蓋引理在一個度量空間中有一族閉球，則這一族球中存在互不相交的球，適合條件
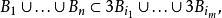5r覆蓋引理
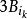5r覆蓋引理
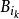5r覆蓋引理 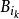5r覆蓋引理表示和有相同中心，而半徑是的三倍的球。
