簡介
龐加萊－林德斯泰特方法（英語：Poincaré–Lindstedt method）是攝動理論中一種當正則攝動法失效時求解常微分方程的近似周期解的方法， 可以在弱非線性振動問題中消除正則攝動法中出現的長期項。
該方法是以數學家昂利·龐加萊與安德斯·林德斯泰特的名字命名的。
攝動理論
攝動理論使用一些特別的數學方法來對於很多不具精確解的問題給出近似解，這些方法從相關的較簡單問題的精確解開始入手。攝動理論將原本問題分為具有精確解的較簡單部分與不具精確解的微擾部分。攝動理論適用的問題通常具有以下性質：通過加入一個微擾項於較簡單部分的數學表述，可以計算出整個問題的近似解。
龐加萊－林德斯泰特方法攝動理論計算出來的解答通常會表達為一個微小參數的冪級數。攝動理論解答與精確解之間的差別，可以用這微小參數來做數量比較。冪級數的第一個項目是精確解的解答。後面的項目描述解答的修正。這修正是因為精確解與原本問題的“完全解”之間的誤差而產生的。更正式地，完全解 的近似可以表達為一個級數：
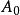龐加萊－林德斯泰特方法
龐加萊－林德斯泰特方法
龐加萊－林德斯泰特方法
龐加萊－林德斯泰特方法在這例子裡， 是簡單又有“精確解”的問題的精確解， 代表由某種系統程式反覆地找到的高階項目修正。因為 的值很微小，這些高階項目修正應該會越來越不重要。
長期變化
長期變化是時間系列在長時期的非周期變化（參見分解時間系列）。無論何者被查覺是長期變化或是與時間尺度無關：在超越世紀的時間尺度上，長期變化在數百萬年的時間尺度下可能是周期變化的一部分。自然界的量往往有周期性和長期變化。當在強調是一種線性的長期變化時，長期變化有時被稱為 或。
