黑利性質

黑利性質是簡單超圖的特殊性質。若取H的節點集X為自然數的集合，邊為X上的算數級數，則H上的黑利性質就是著名的中國剩餘定理，或稱孫子定理。

簡介

黑利性質是簡單超圖的特殊性質。

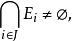黑利性質

設H=(E,E,...,E)是一個簡單超圖，若對於任何J⊂{1,2,...,m}，從條件對任何i,j∈J，E∩E≠∅可以導出條件則稱H滿足黑利性質。

適用範圍

若H的節點集由一條直線上所有點組成，它的邊集為這條直線中的一些區間，則稱H為一個區間超圖。黑利(Helly,E.)的一個定理指出這種超圖具有上述性質，這也就是稱之為黑利性質的緣由。

若取H的節點集X為自然數的集合，邊為X上的算數級數，則H上的黑利性質就是著名的中國剩餘定理，或稱孫子定理。

k黑利性質

一個簡單超圖H=(E,E,...,E)，若對於任何J⊂{1,2,...,m}滿足性質：

黑利性質

1、對任何I⊂J，從|I|≤k可導出，

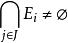黑利性質

2、，

則稱它有k黑利性質。

黑利性質就是指2黑利性質。