高分子鏈的構象統計
正文
用統計力學的方法處理假設的模型鏈的構象，以計算依賴於構象的各種性質，例如鏈的均方末端距、轉動半徑、偶極矩、光學各向異性、光譜二向色性等。分子鏈可視為統計力學的一個巨觀“小體系”，上述性質表征其巨觀態，而構象（由鏈中每個鍵的內鏇轉角決定）則代表微觀態，其數目稱構象數。自由連線鏈 是在1934年由W.庫恩最早提出的統計模型,其數學基礎是所謂無規飛行問題,把它簡化為二維時就是無規行走問題，所以自由連線鏈也稱無規飛行鏈。在此模型中，假定高分子鏈是由n個長度為l的且不占體積的剛性統計單元組成,相鄰的兩單元間自由連線,即每一單元在空間中不依賴於前一單元而無規取向。根據無規飛行數學理論，得到鏈兩端距離的均方值
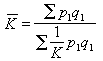(均方末端距)為: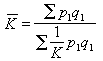＝nl2。當n＝104時,鏈的均方根末端距
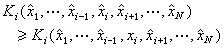只有整個鏈朝一個方向完全伸直時的末端距(hmax＝nl)的1％,可見分子鏈是十分捲曲的。這種分子形態可比擬為亂的毛線團，因此通常稱為無規線團。當統計單元數目很大時，鏈端分布函式具有高斯幾率函式的形式，因此這種模型又稱高斯統計線團，簡稱高斯鏈。 根據統計熱力學的玻耳茲曼公式可將高分子鏈的構象熵與該鏈在空間一切可取的構象數聯繫起來，捲曲形態鏈的構象數大，相應的構象熵也大。由熵增原理可知，孤立鏈在無外力作用下總是自髮捲曲的，這就是高分子長鏈柔性的實質。橡膠的高彈性主要由形變中高分子鏈構象熵的改變所決定，歷史上鏈構象統計理論首先在橡膠彈性物理中得到套用和發展。
由於自由連線鏈模型幾乎喪失了與實際化學結構的聯繫，難以定量地描述真實鏈，所以必須進行修正。這一工作涉及給定鍵長和鍵角，並包括自由或受阻內鏇轉模型鏈的構象。在較短鏈的構象,剛性鏈的棒狀構象,多肽、蛋白質或核酸的螺鏇構象，酶的球狀構象方面，已發展了其他模型。
內鏇轉異構體模型 按照統計力學的基本原理，計算長鏈分子的性質必須對全部構象進行平均，若考慮每個單鍵鏇轉的連續變化，這種計算實在太困難。1951年М.Β.沃爾肯斯坦根據小分子有機化合物內鏇轉的研究，提出內鏇轉異構體模型，對每一內鏇轉角只設一些離散狀態的數值，並從不同狀態間的能量差值，估算不同狀態出現的統計權重，使這一任務大為簡化了。通常假定每個鍵適合的內鏇轉狀態的數目為 3（反式、左式和右式），對於含103個鍵的分子鏈,其總構象數將多達31000（約1.3×10477）個。用內鏇轉異構體模型處理高分子鏈的優點是：在概念和原理上直截了當，但由於相鄰鍵鏇轉的相互依賴，使這一模型的套用比較複雜。P.J.弗洛里在沃爾肯斯坦等人工作的基礎上深入處理了孤立單鏈的構象統計。他採用半經驗公式，估算出鏇轉異構體的勢能面，從而為定量表述鍵相互依賴的受阻內鏇轉提供了依據，得出了與實驗一致的結果。他提出一種普遍適用的系統化的方法──生成元矩陣法，採用矩陣連乘即可具體計算各種構象的平均性質，並在此基礎上對分子鏈尺寸以及依賴於構象的其他性質進行了理論和實驗的研究。
大型電子計算機的套用為鏈構象統計理論計算的發展提供了新的機會。例如，在計算鏈構象時，每個鍵的構象可由隨機數決定，同時考慮到各種不同的構象的條件幾率。這種計算機產生的構象既包含了鍵長、鍵角等幾何參數，也考慮了近鄰相互作用，可以說這種模型鏈與真實分子鏈已經十分接近了。
