背景
從理論上說，貝葉斯推斷和分析是容易實施的，即對於任何先驗分布，只需要計算所需後驗分布的性質，如後驗分布的矩(如後驗均值、後驗方差)、後驗機率密度函式等，而這些計算本質上就是計算後驗分布某一函式的高維積分。但在實踐中，鑒於未知參數的後驗分布多為高維、複雜的非常見分布，對這些高維積分進行計算十分困難，這一困難使得貝葉斯推斷方法在實踐中的套用受到很大的限制，在很長一段時間，貝葉斯推斷主要用於處理簡單低維的問題，以避免計算上的困難。MCMC方法突破了這一原木極為困難的計算問題，它通過模擬的方式對高維積分進行計算，進而使原本異常複雜的高維積分計算問題迎刃而解，使貝葉斯方法僅適用於解決簡單低維問題的狀況大有改觀為貝葉斯方法的套用開闢了新的道路。
基本思路結構
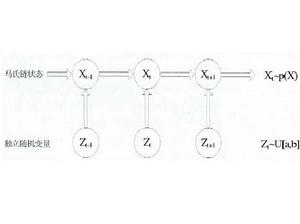
圖1 MCMC方法框架圖MCMC方法的結構如圖1所示。
MCMC方法是使用馬爾科夫鏈的蒙特卡洛積分，其基木思想是：構造一條Markov鏈，使其平穩分布為待估參數的後驗分布，通過這條馬爾科夫鏈產生後驗分布的樣木，並基於馬爾科夫鏈達到平穩分布時的樣木(有效樣本)進行蒙特卡洛積分。
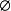馬爾科夫鏈蒙特卡洛方法設 為某一空間，n為產生的總樣木數，m為鏈條達到平穩時的樣本數，則MCMC方法的基木思路可概括為：
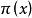馬爾科夫鏈蒙特卡洛方法(1)構造Markov鏈。構造一條Markov鏈，使其收斂到平穩分布 ；
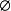馬爾科夫鏈蒙特卡洛方法
馬爾科夫鏈蒙特卡洛方法
馬爾科夫鏈蒙特卡洛方法(2)產生樣本：由 中的某一點 出發，用(1)中的Markov鏈進行抽樣模擬，產生點序列： ；
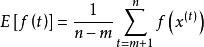馬爾科夫鏈蒙特卡洛方法(3)蒙特卡洛積分：任一函式f(x)的期望估計為： 。
MCMC中採樣算法如圖2所示。
圖2方法
在採用MCMC方法時，馬爾科夫鏈轉移核的構造至關重要，不同的轉移核構造方法，將產生不同的MCMC方法，目前常用的MCMC方法主要有兩種：Gibbs抽樣和Metropolis-Hastings算法。
Metropolis-Hasting 算法
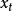馬爾科夫鏈蒙特卡洛方法Metropolis 算法是馬爾科夫鏈蒙特卡羅的基石。它是由 Metropolos 等人在 1953年的一篇僅 4 頁的文章中提出。Metropolis 算法用一個對稱的建議分布 T(x,y)來產生一個潛在的轉移點，然後根據特定的接受拒絕方法來決定是否轉移到該潛在點。最初的 Metropolis 算法將 T 取為對稱的函式，而 Metropolis-Hasting 方法將之推廣到非對稱的 T，其中 T 滿足 T(x,y)>0 的充要條件是 T(y,x)>0。已知當前狀態 ，該算法的疊代步驟如下：
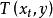馬爾科夫鏈蒙特卡洛方法第 1 步：從建議分布 抽取潛在轉移點 y。
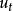馬爾科夫鏈蒙特卡洛方法
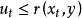馬爾科夫鏈蒙特卡洛方法
馬爾科夫鏈蒙特卡洛方法
馬爾科夫鏈蒙特卡洛方法第 2 步：在[0,1]均勻分布中抽取一個隨機數 ，並且更新 ，若滿足 ，否則令 。對於 r(x,y)，Metropolis 和 Hastings 建議採用如下形式的：
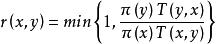馬爾科夫鏈蒙特卡洛方法Gibbs 算法
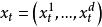馬爾科夫鏈蒙特卡洛方法 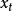馬爾科夫鏈蒙特卡洛方法 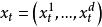馬爾科夫鏈蒙特卡洛方法
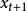馬爾科夫鏈蒙特卡洛方法Gibbs 算法是一種特殊的 Metropolis 算法。對於一個 d 維隨機變數 ，Gibbs 算法在生成 的第 i 個分量時選擇建議分布 T 為第 i 個分量基於其他所有分量的條件分布。即已知當前狀態 ， Gibbs 算法通過如下的方法更新 d 個分量來更新 ：
馬爾科夫鏈蒙特卡洛方法
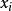馬爾科夫鏈蒙特卡洛方法
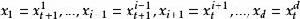馬爾科夫鏈蒙特卡洛方法
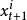馬爾科夫鏈蒙特卡洛方法第 1 步 ： 對 於 固 定 的 i（初值為1），從條件分件 =( | )中抽樣出 。
第 2 步：令 i=i+1，重複第 1 步。
收斂診斷方法
MCMC方法依賴於模擬的收斂性，下面介紹三種常用的收斂性診斷方法。
同時產生多條馬爾科夫鏈
這種方法的思路是選取多個不同的初值，同時產生多條馬爾科夫鏈，經過一段時間後，若這幾條鏈穩定下來，則說明算法收斂了。在實際操作中，可在同一個二維圖中畫出這些不同的馬爾科夫鏈產生的後驗樣本值對疊代次數的散點圖，如果經過若干次疊代後，這些散點圖基木穩定，重合在一起，則可判斷其算法收斂。
比率診斷法
馬爾科夫鏈蒙特卡洛方法
馬爾科夫鏈蒙特卡洛方法這種方法的思路是選取多個不同的初值，同時產生T條馬爾科夫鏈，記第j條鏈的方差估計為 ，鏈內方差的均值為W，鏈間方差為B，則： 。R的值趨近1，則表明MCMC模擬收斂，且比較穩定，通常R<1.2，表明收斂性較好；如果R值很大，則表明需要增大模擬的次數，且考慮收斂速度慢的原因。
Teweke Test法
Teweke Test由一系列的Z檢驗組成，其基木思路是：先對所有樣本(假設有M個)做一次Z檢驗，然後去掉最前面的c個樣本，用剩餘的M-c個樣本重複上述檢驗，再繼續去掉最前面的c個樣本，用剩餘的M-2c個樣本重複上述檢驗，依次類推，重複K次這樣的檢驗，直到M-Kc<50時終止檢驗，觀察這K次Z檢驗的z值，若大部分z值都落在(-2,2)內，則表明馬爾科夫鏈己收斂到平穩分布。
