簡介
MCMC方法是使用馬爾科夫鏈的蒙特卡羅積分，其基本思想是：構造一條Markov鏈使其平穩分布為待估參數的後驗分布，通過這條馬爾科夫鏈產生後驗分布的樣本，並基於馬爾科夫鏈達到平穩分布時的樣本（有效樣本）進行蒙特卡羅積分。因於初始樣本，最常見的MCMC取樣只能近似得到分布。複雜的MCMC改進算法如過往耦合，但是會消耗更多的計算資源和時間。典型用法是模擬一個隨機行走的行人來進行路徑最佳化等。每一步都算作是一個狀態。而統計經過次數最多的地方將在下一步中更有可能為目的地。MCMC 算法收斂性特徵為全局性最小，對應的線性最小二乘法則容易在局部收斂情況下停滯或者由於非線性問題收斂緩慢，同時大量的套用表明 MCMC 方法明顯優於線性模型。
馬氏蒙特卡洛方法是一種結合了蒙特卡羅法的解決方案。但不同於以往的蒙特卡洛integration是統計獨立的，MCMC中的是統計相關的。在採用MCMC方法時馬爾科夫鏈轉移核的構造至關重要，不同的轉移核構造方法將產生不同的MCMC方法，常用的MCMC方法主要有兩種Gibbs抽樣和Metropo-Lis-Hastings算法。MCMC已經被廣泛地套用於統計分析圖像處理、信號處理、金融分析等領域。
常見算法
Gibbs抽樣
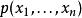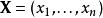馬爾科夫蒙特卡洛
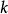馬爾科夫蒙特卡洛
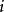馬爾科夫蒙特卡洛
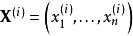馬爾科夫蒙特卡洛
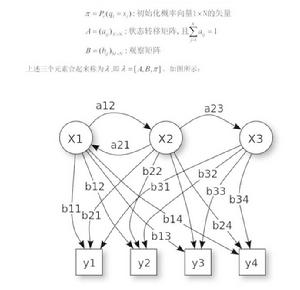
馬爾科夫蒙特卡洛吉布斯採樣（英語：Gibbs sampling）是統計學中用於馬爾科夫蒙特卡洛（MCMC）的一種算法，用於在難以直接採樣時從某一多變數機率分布中近似抽取樣本序列。該序列可用於近似聯合分布、部分變數的邊緣分布或計算積分（如某一變數的期望值）。某些變數可能為已知變數，故對這些變數並不需要採樣。吉布斯採樣常用於統計推斷（尤其是貝葉斯推斷）之中。這是一種隨機化算法，與最大期望算法等統計推斷中的確定性算法相區別。與其他MCMC算法一樣，吉布斯採樣從馬爾科夫鏈中抽取樣本，可以看作是Metropolis–Hastings算法的特例。該算法的名稱源於約西亞·威拉德·吉布斯，由斯圖爾特·傑曼與唐納德·傑曼兄弟於1984年提出。吉布斯採樣適用於條件分布比邊緣分布更容易採樣的多變數分布。假設我們需要從聯合分布 中抽取 的 個樣本。記第 個樣本為 。吉布斯採樣的過程則為：
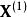馬爾科夫蒙特卡洛確定初始值 。
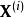馬爾科夫蒙特卡洛
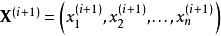馬爾科夫蒙特卡洛
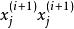馬爾科夫蒙特卡洛
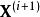馬爾科夫蒙特卡洛
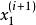馬爾科夫蒙特卡洛
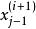馬爾科夫蒙特卡洛 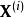馬爾科夫蒙特卡洛
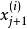馬爾科夫蒙特卡洛
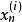馬爾科夫蒙特卡洛
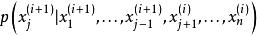馬爾科夫蒙特卡洛假設已得到樣本 ，記下一個樣本為 。於是可將其看作一個向量，對其中某一分量 ，可通過在其他分量已知的條件下該分量的機率分布來抽取該分量。對於此條件機率，我們使用樣本 中已得到的分量 到 以及上一樣本 中的分量 到 ，即 。
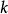馬爾科夫蒙特卡洛重複上述過程 次。
在採樣完成後，我們可以用這些樣本來近似所有變數的聯合分布。如果僅考慮其中部分變數，則可以得到這些變數的邊緣分布。此外，我們還可以對所有樣本求某一變數的平均值來估計該變數的期望。
梅特羅波利斯－黑斯廷斯算法
梅特羅波利斯－黑斯廷斯算法（Metropolis–Hastings algorithm）是統計學與統計物理中的一種馬爾科夫蒙特卡洛（MCMC）方法，用於在難以直接採樣時從某一機率分布中抽取隨機樣本序列。得到的序列可用於估計該機率分布或計算積分（如期望值）等。梅特羅波利斯－黑斯廷斯或其他MCMC算法一般用於從多變數（尤其是高維）分布中採樣。對於單變數分布而言，常會使用自適應判別採樣（adaptive rejection sampling）等其他能抽取獨立樣本的方法，而不會出現MCMC中樣本自相關的問題。該算法的名稱源於美國物理學家尼古拉斯·梅特羅波利斯與加拿大統計學家W·K·黑斯廷斯。
馬爾可夫鏈
馬爾可夫鏈，因安德烈·馬爾可夫（A.A.Markov，1856－1922）得名，是指數學中具有馬爾可夫性質的離散事件隨機過程。該過程中，在給定當前知識或信息的情況下，過去（即當前以前的歷史狀態）對於預測將來（即當前以後的未來狀態）是無關的。
在馬爾可夫鏈的每一步，系統根據機率分布，可以從一個狀態變到另一個狀態，也可以保持當前狀態。狀態的改變叫做轉移，與不同的狀態改變相關的機率叫做轉移機率。隨機漫步就是馬爾可夫鏈的例子。隨機漫步中每一步的狀態是在圖形中的點，每一步可以移動到任何一個相鄰的點，在這裡移動到每一個點的機率都是相同的（無論之前漫步路徑是如何的）。馬爾可夫在1906年首先做出了這類過程。而將此一般化到可數無限狀態空間是由柯爾莫果洛夫在1936年給出的。
馬爾可夫鏈通常用來建模排隊理論和統計學中的建模，還可作為信號模型用於熵編碼技術，如算術編碼（著名的LZMA數據壓縮算法就使用了馬爾可夫鏈與類似於算術編碼的區間編碼）。馬爾可夫鏈也有眾多的生物學套用，特別是人口過程，可以幫助模擬生物人口過程的建模。隱蔽馬爾可夫模型還被用於生物信息學，用以編碼區域或基因預測。
