頻率分布直方圖

在直角坐標系中，橫軸表示樣本數據的連續可取數值，按數據的最小值和最大值把樣本數據分為m組，使最大值和最小值落在開區間（a，b）內，a略小於樣本數據的最小值，b略大於樣本數據的最大值。組距為d=（b-a）/m，各數據組的邊界範圍按左閉右開區間，如[a，a+d），[a+d，a+2d),……[a+（m-1）d，b），縱軸表示頻率除以組距（落在各組樣本數據的個數稱為頻數，頻數除以樣本總個數為頻率）的值，以頻率和組距的商為高、組距為底的矩形在直角坐標繫上來表示，由此畫成的統計圖叫做頻率分布直方圖。

基本信息

• 中文名：頻率分布直方圖

• 縱軸表示：頻率除以組距
• 橫軸表示：樣本數據的連續可取數值
• 眾數：圖中最高矩形中點的橫坐標

基本概念

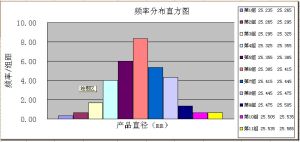頻率分布直方圖

在直角坐標系中，橫軸表示樣本數據，縱軸表示頻率與組距的比值，將頻率分布表中各組頻率的大小用相應矩形面積的大小來表示，由此畫成的統計圖叫做頻率分布直方圖。（在圖中，各個長方形的面積等於相應各組的頻率的數值，所有小矩形面積和為1）
把全體樣本分成的組的個數稱為 組數。每一組兩個端點的差稱為組距。落在不同小組中的數據個數為該組的 頻數。各組的頻數之和等於這組數據的總數。頻數與數據總數的比為頻率（總頻率=各組頻率之和，且它的值為1）。頻率大小反映了各組頻數在數據總數中所占的份量。

運用

頻率分布直方圖

頻率分布直方圖能清楚顯示各組頻數分布情況又易於顯示各組之間頻數的差別。它主要是為了將我們獲取的數據直觀、形象地表示出來，讓我們能夠更好了解數據的分布情況，因此其中組距、組數起關鍵作用。分組過少，數據就非常集中；分組過多，數據就非常分散，這就掩蓋了分布的特徵。當數據在100以內時，一般分5~12組為宜。
從頻率分布直方圖可以求出的幾個數據：
眾數：頻率分布直方圖中最高矩形的底邊中點的橫坐標。
平均數：頻率分布直方圖各個小矩形的面積乘底邊中點的橫坐標之和。
中位數：把頻率分布直方圖分成兩個面積相等部分的平行於Y軸的直線橫坐標。

畫圖步驟

1．找出所有數據中的最大值和最小值，並算出它們的差（極差）。
2．決定組距和組數。
3．確定分點。
4．將數據以表格的形式列出來。
5．畫頻數分布直方圖。
與頻率分布直方圖相關的一種圖為折現圖。我們可以在直方圖的基礎上來畫，先取直方圖各矩形上邊的中點，然後在橫軸上取兩個頻數為0的點，這兩點分別與直方圖左右兩端的兩個長方形的組中值相距一個組距，將這些點用線段依次聯結起來，就得到了頻數分布折線直方圖。