定義
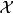 預解方程
預解方程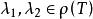 預解方程
預解方程設 T 是作用在巴拿赫空間 上的有界線性運算元 ,當時,預解方程為
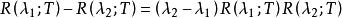 預解方程
預解方程預解式
一元二次方程
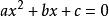 預解方程
預解方程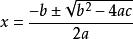 預解方程
預解方程普通一元二次方程的預解方程,在9世紀時就已經發現。在中,。
目前國中二年級課本中有相關描述。
一元三次方程
16世紀,普通一元三次方程及一元四次方程的預解方程都被發現。
該預解方程推倒的主旨思想是通過換元將n次方程向(n-1)次方程轉變,再用解(n-1)次方程的預解方程推出該方程預解式。
1505年,三次方程式預解方程已被Scipio Ferreo求出,之後馮塔納也求出預解方程,並以嚴守秘密為條件傳授給了卡爾丹,但卡爾丹不守信約,於1545年發表,後人稱之為卡爾丹公式。之後Hudde於1650年發表了另一種解法。
四次方程式預解式由費拉里於1540年前後推出。
一元四次以上方程
1770年,拉格朗日將前人方法總結,並間接使用置換群的概念(尚未提出),將各種解法歸納於一種原理下, 並證明普通五次方程沒有預解方程,自此,近世代數拉開序幕。
1815年,柯西對置換進行了系統的研究,成為了置換群理論研究的先驅。
此後,阿貝爾、伽羅瓦兩位天才數學家證明了n(n>4)次方程式沒有有理與無理預解方程,並提出群論、域論這兩個重要的數學概念,為日後的代數學研究奠下重要的基石。但這兩個數學家都英年早逝,伽羅瓦20歲時因決鬥逝去,阿貝爾27歲染重疾逝去,他們死後約半個世紀,他們的學說才被認同。

