介紹
第n項測試（ the n-th term test for divergence）是數學上測試無窮級數是否發散的一個方式。
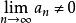項測試
項測試若 或極限不存在，則 發散。
用途
項測試和其他較強的收斂測試不同，此測試方式只能確認級數是否發散，不能確認級數是否收斂。若不符合此測試的條件，無法判定級數是收斂或是發散。例如：
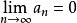項測試 項測試若 ， 則 可能收斂也可能發散，此條件下無法用此測試判定級數是否收斂。
調和級數就是不符合此測試的發散條件，卻又是發散級數的典型範例。調和級數是以下p級數的特例：
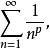項測試配合項測試及其他測試，可得到以下的結果：
•若p≤ 0，根據項測試可知此級數發散。
•若0
•若1
證明
要證明此測試法，一般都會證明其逆否命題（contrapositive）形式；
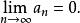項測試
項測試若 收斂，則 。
利用極限證明
若 s是級數的部分和，則上述對數列的假設可推得
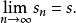項測試因此可得
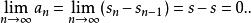項測試柯西判別法
項測試級數收斂的假設表示級數可以滿足柯西判別法的測試：對任 均存在一數字 N使得
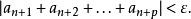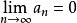項測試 項測試在所有 n> N及 p≥ 1的條件下均成立。令 p= 1，即可得到。
套用範圍
項測試最簡單的版本可以用在實數的無窮級數中。上述的二個證明也可以在適用在賦范向量空間中。
