兩種廣義的非線性卷積
高階卷積
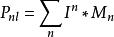非線性卷積層
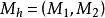非線性卷積層高階卷積在運算中除了考慮圖像的一階變換，還引入了更高階變換，用以擴展卷積模型的擬合範圍，其過程可以表達為 ，然而，過高的階數會造成計算的不穩定和低效，因此一般用到2階信息，即高階卷積核為 。
置換卷積
置換卷積.一般卷積變換都具有空間位移不變性，即變換僅發生在亮度空間而不改變空間位置，因此它們所模擬的圖像風格必須滿足坐標對齊性質。置換卷積定義為不改變圖像的亮度而僅僅改變像素位置。置換卷積核中每個元素為一置換向量,通過該向量將像素坐標映射到新的位置.具體表示為
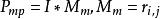非線性卷積層
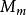非線性卷積層對於大多數的圖像過程，置換向量都不是固定常量，而是一個隨機向量，因此需要計算置換向量的平均值來確定置換卷積核 。
卷積核的估計
高階核估計
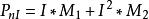非線性卷積層
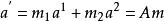非線性卷積層高階卷積核是普通卷積核的推廣,因此其估計算法也與一般核估計算法相近。高階卷積過程為 ，對於訓練集合A和A'來說，，將其展成向量形式為 。此問題是一個典型的過靜定問題,最簡便的解法是最小二乘法。為增強穩定性，利用Tikhonov正則化將其變為最小化問題
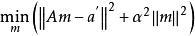非線性卷積層
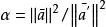非線性卷積層
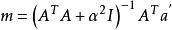非線性卷積層其中設定 ,該最佳化問題在全局空間的解為 。推廣到2階空間，並要求m1非負，在這些約束下，最佳解可以採用疊代計算方式求出：
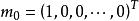非線性卷積層step1.初始化： ；
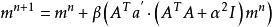非線性卷積層step2.計算
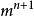非線性卷積層
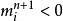非線性卷積層
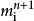非線性卷積層step3.掃描 ，若 ，則令 =0
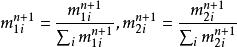非線性卷積層step4.重新正則化，
非線性卷積層 非線性卷積層其中 是調節因子，可以調控收斂速度，一般取 =0.5..當疊代的相鄰誤差較小時,就可以終止疊代, 輸出結果。
置換核估計
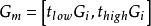非線性卷積層
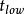非線性卷積層
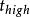非線性卷積層 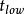非線性卷積層 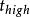非線性卷積層由於置換作用僅僅改變像素位置,因此可以採用搜尋的辦法估計置換核在搜尋域內為每個像素尋找置換向量,搜尋域分為初始域G和置換域Gm.設 ,其中 和 分別是內外比例限參數,取 =05, =2。在Gm中以柵格順序進行匹配搜尋,匹配距離定義為色彩空間的歐氏距離.如圖1所示,由於圖像的亮度信號重要性遠遠超過色差信號,為了加快搜尋計算速度,我們用和文獻7中同樣的思路,將RGB圖像變換至YUV空間,並在Y空間計算匹配距離。
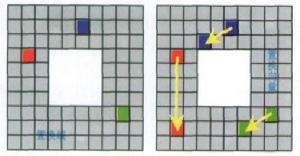置換方式示意圖
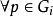非線性卷積層
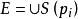非線性卷積層
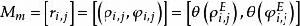非線性卷積層
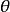非線性卷積層具體地,對 ,設其匹配集合為 ，將各個匹配集合中所有數據均引入置換向量庫,得到最後的統計樣本 ;則置換核為 ,其中 是數學期望。
.高階核估計的前提是沒有顯著的置換髮生; 而置換核計算的前提正好相反,兩者相互對立，要確定完整的卷積模型必須解決這個矛盾，可以採用多解析度方式加以處理。
