非參數判別
採用貝葉斯決策，需要對機率分布進行估計，然後通過最大似然或者貝葉斯估計的方法估計其分布的參數，然後在通過貝葉斯分類器進行分類，這種方法叫做 參數判別方法。
然而實際上，對樣本分布的估計往往是不準確的，也是比較困難的。針對不同的情況，設計不同的分類器，這種方法不通過分布假設、參數估計，而是根據樣本信息直接設計分類器，這種方法叫做 非參數判別方法。
線性分類器
設樣本d在維特徵空間中描述，則兩類別問題中線性判別函式的一般形式可表示成
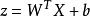非參數決策規則
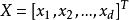非參數決策規則
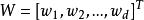非參數決策規則其中， , ，b是閾值，常數。
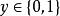非參數決策規則
非參數決策規則 非參數決策規則
非參數決策規則以二分類任務為例，將輸出標記為 ，而 是實值，於是將實值 轉化為 值，最理想的是“單位階躍函式”：
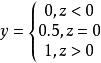非參數決策規則相應的決策規則可表示成：
若預測值z大於零，判為正例；
若預測值z小於零，判為反例；
若預測值z為臨界值零，可判為任意。
線性判別分析
線性判別分析（Linear Discriminant Analysis，簡稱LDA）是一種經典的線性學習方法，在二分類問題上因為最早由Fisher提出，亦稱“Fisher判別分析”。
LDA的思想非常樸素：給定訓練樣例集，設法將樣例投影到一條直線上，使得同類樣例的投影點儘可能接近、異類樣本儘可能遠離；在對新樣本進行分類時，將其投影到同樣的這條直線上，再根據其投影點的位置來確定新樣本的類別。
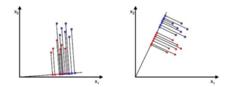圖1 樣本點投影從直觀上來看，右圖比較好，可以很好地將不同類別的樣本點分離。接下來我們從定量的角度來找到這個最佳的w。首先我們尋找每類樣例的均值（中心點），這裡i只有兩個
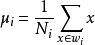非參數決策規則由於x到w投影后的樣本點均值為
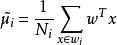非參數決策規則由此可知，投影后的的均值也就是樣本中心點的投影。
什麼是最佳的直線（w）呢？
同類樣例的投影點儘可能接近、異類樣本儘可能遠離的直線就是好的直線。
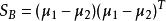非參數決策規則對投影后的類求散列值（scatter），如下：
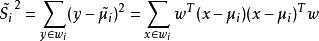非參數決策規則
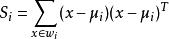非參數決策規則定義
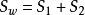非參數決策規則定義 ，
則J(w)最終可以表示為：
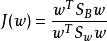非參數決策規則
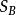非參數決策規則
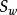非參數決策規則上式即為LDA欲最大化的目標，即 和 的“廣義瑞利商”。
決策規則：
在對新樣本進行分類時，將其投影到同樣的這條直線上，再根據其投影點的位置來確定新樣本的類別。
感知器
感知機學習旨在求出將訓練數據集進行線性劃分的分類超平面，為此，導入了基於誤分類的損失函式，然後利用梯度下降法對損失函式進行極小化，從而求出感知機模型。感知機模型是神經網路和支持向量機的基礎。
感知機模型如下：
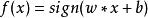非參數決策規則其中，x為輸入向量，sign為符號函式，括弧裡面大於等於0，則其值為1，括弧裡面小於0，則其值為-1。w為權值向量，b為偏置。
求感知機模型即求模型參數w和b。
感知機預測，即通過學習得到的感知機模型，對於新的輸入實例給出其對應的輸出類別1或者-1。
與線性分類器類似。
支持向量機
支持向量機(Support Vector Machine，SVM)是Corinna Cortes和Vapnik等於1995年首先提出的，它在解決小樣本、非線性及高維模式識別中表現出許多特有的優勢，並能夠推廣套用到函式擬合等其他機器學習問題中。在機器學習中，支持向量機（SVM，還支持矢量網路）是與相關的學習算法有關的監督學習模型，可以分析數據，識別模式，用於分類和回歸分析。
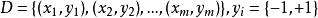非參數決策規則給定訓練樣本集 ,分類學習的基本思想時：基於數據集D再樣本空間中找到一個超平面，將不同類別的樣本分開，但能找到的這個超平面可能有很多，如何去確定哪一個最好呢？
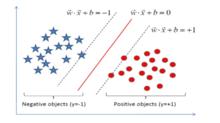圖2 支持向量機分類直觀上來看，應該尋找位於兩個訓練樣本“正中間：的劃分超平面，即圖2中紅色的那個，因為該超平面對訓練樣本的局部擾動的”容忍“性最好。在樣本空間中，劃分超平面可通過如下線性方程來描述：
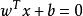非參數決策規則
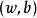非參數決策規則樣本空間任意點x到超平面的距離可寫為：
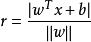非參數決策規則
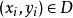非參數決策規則
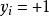非參數決策規則
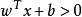非參數決策規則
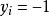非參數決策規則
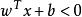非參數決策規則假設超平面能將訓練樣本正確分類，即，對於，若 ，則有；若，則有。
距離超平面最近的幾個點被稱為”支持向量“，兩個異類支持向量到超平面的距離之和為：
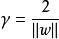非參數決策規則它被稱為“間隔”
欲找到具有最大間隔的劃分超平面，也就是要滿足以下條件：
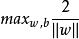非參數決策規則
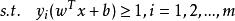非參數決策規則決策規則：
非參數決策規則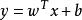
非參數決策規則在對新樣本 進行預測分類時，計算，若y>0，則預測為正例；若y<0時，則預測為反例。
