簡介
概述
非切向邊界值是區域上的函式當限制自變數以某種特殊方式趨近於邊界點時的極限。
具體內容
設D⊂R (n≥2)是一個李普希茨區域，即D為有界域且滿足條件：對每點Q∈∂D，對應一個局部坐標系(X,y)，X∈R ，y∈R ，及一個鄰域N和函式b(X)，使得：
1、|b(X)-b(X')|≤k|X-X'|（k為常數）；
2、N∩D=N∩{(X,y)|y≥b(X)}；
3、N∩∂D=N∩{(X,y)|y=b(X)}。
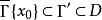非切向邊界值設f是D上定義的函式，如果當x沿著任何一個以x∈∂D為頂點的內錐Γ（即存在一個以x為頂點的錐Γ'使得 ）趨於x時，f(x)有同一個極限值，就稱f在x有非切向邊界值（角極限）。
極限
“極限”是數學中的分支——微積分的基礎概念，廣義的“極限”是指“無限靠近而永遠不能到達”的意思。
數學中的“極限”指：某一個函式中的某一個變數，此變數在變大（或者變小）的永遠變化的過程中，逐漸向某一個確定的數值A不斷地逼近而“永遠不能夠重合到A”（“永遠不能夠等於A，但是取等於A‘已經足夠取得高精度計算結果）的過程中，此變數的變化，被人為規定為“永遠靠近而不停止”、其有一個“不斷地極為靠近A點的趨勢”。極限是一種“變化狀態”的描述。此變數永遠趨近的值A叫做“極限值”（當然也可以用其他符號表示）。
