概念
電子作為帶電粒子在磁場中運動會受到洛倫茲力的作用,軸旋轉對稱磁場可以使運動著的電子折射而發生“聚焦”,像可見光通過玻璃透鏡一樣用來成像。用電磁線圈可以產生軸旋轉對稱磁場,把這種能對運動電子聚焦成像的裝置稱為“電磁透鏡”或“磁透鏡”。
 電磁透鏡
電磁透鏡圖1-1所示的通電短線圈就是一個簡單的電磁透鏡,磁感應強度 由電流方向決定。
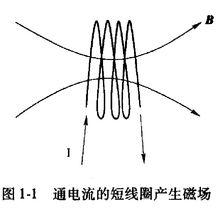 圖1-1
圖1-1 電磁透鏡
電磁透鏡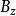 電磁透鏡
電磁透鏡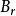 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡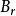 電磁透鏡
電磁透鏡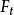 電磁透鏡
電磁透鏡圖1-2是電磁透鏡聚焦原理示意圖。磁透鏡造成一種軸對稱不均勻分布的磁場,磁力線圍繞導線呈環狀,磁力線上任意一點的磁感應強度 都可以分解成平行於透鏡主軸的分量 和垂直於主軸的分量 。速度為 平行於透鏡主軸的電子進入透鏡的磁場時,位於透鏡上半部Ⅰ點的電子受到垂直分量 的作用,使電子受到切向力。根據左手法則,電子所受的切向力 的方向如圖1-2所示。
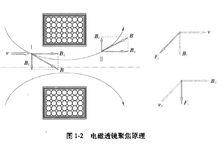 圖1-2
圖1-2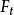 電磁透鏡
電磁透鏡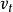 電磁透鏡
電磁透鏡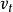 電磁透鏡
電磁透鏡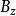 電磁透鏡
電磁透鏡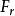 電磁透鏡
電磁透鏡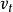 電磁透鏡
電磁透鏡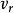 電磁透鏡
電磁透鏡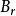 電磁透鏡
電磁透鏡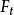 電磁透鏡
電磁透鏡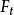 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡使電子獲得切向速度 , 隨即和 分量叉乘,形成了另一個向透鏡主軸靠近的徑向力 ,使電子向主軸偏轉。平行入射到磁場中的電子到達不同的位置,都得到切向速度 使電子做圓周運動,同時都具有軸向速度 使電子趨向軸上的一點。當電子穿過線圈運動到透鏡的下半部Ⅱ點位置時, 的方向改變了180°, 隨之反向,但是 的反向只能使 變小,而不能改變其方向。因此穿過線圈的電子仍然向主軸靠近。電子的運動軌跡是原來平行於主軸的直線運動、圓周運動和向軸運動的合運動,整體軌跡是圓錐螺旋狀,最終落到磁透鏡的軸上,完成電子的磁聚焦。
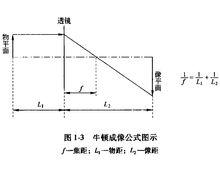 圖1-3
圖1-3一束平行於主軸的入射電子束通過電磁透鏡時被聚焦在軸線上一點,這一點稱為焦點,這與光學玻璃凸透鏡對平行於透鏡主軸入射的平行光的聚焦作用十分相似,仍可用牛頓成像公式來說明這一聚焦過程。見圖1-3。
電磁透鏡的像差
按照衍射理論計算結果,光學透鏡的解析度是波長的一半。對於電磁透鏡來說,目前還遠遠沒有達到這一水平。主要原因是除了衍射效應對解析度的影響外,還有像差對解析度的影響。電磁透鏡的主要像差有球差、像散和色差。
球差
 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡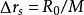 電磁透鏡
電磁透鏡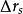 電磁透鏡
電磁透鏡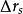 電磁透鏡
電磁透鏡球差是由電磁透鏡近軸區域磁場和遠軸區域磁場對電子束的折射能力不同而產生的像差。近軸區域對電子束的折射能力弱,遠軸區域對電子束的折射能力強。來自於軸上物點散射的電子束,經過電磁透鏡折射後到達像平面本應該形成一個對應的像點,但實際上近軸電子和遠軸電子不聚焦在同一點上(圖1-4),這種由於透鏡磁場折射能力不同形成的像點發散就是球差。像平面上沿軸線從遠軸電子聚焦點到近軸聚焦點之間,存在一個像平面,其上的散焦斑最小,同其他各處的圓斑相比,這個散焦斑最清晰,就把最小散焦斑作為與物點對應的像點。設散焦斑半徑為 ,將 除以放大倍數 把最小散焦斑折算到物平面上,有 ,原來的物點由於球差的影響變成了半徑為 的漫散圓斑,用 表示球差大小,按照物理光學的相關公式,有:
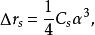 電磁透鏡
電磁透鏡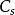 電磁透鏡
電磁透鏡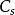 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡式中, 為球差係數,通常情況下電磁透鏡的球差係數 相當於它的焦距,大小約為1~3mm; 為孔徑半角。由上式可見,減小球差係數和孔徑半角可以減小球差,尤其是孔徑半角減小時,球差顯著減小。
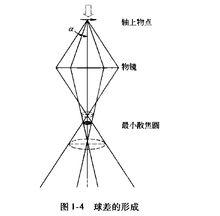 圖1-4
圖1-4球差是影響電磁透鏡解析度的主要像差,它不能像光學透鏡那樣通過設計凸透鏡、凹透鏡的組合來補償消除。但最近發明的電磁透鏡球差矯正器可以有效地降低球差係數。
像散
像散是由透鏡磁場的非旋轉對稱引起的像差。透鏡的極靴孔加工誤差,上、下極靴的軸線錯位、極靴材質不均以及極靴孔周圍的局部污染等,都會引起透鏡的磁場產生橢圓度。橢圓磁場長、短軸方向上的聚焦能力存在差異,結果成像物點通過透鏡後不能在像平面上聚焦於一點(圖1-5)。
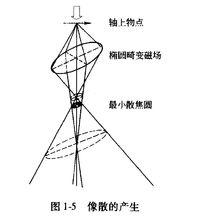 圖1-5
圖1-5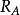 電磁透鏡
電磁透鏡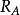 電磁透鏡
電磁透鏡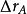 電磁透鏡
電磁透鏡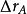 電磁透鏡
電磁透鏡同樣在長、短軸聚焦點之間有一個最佳聚焦位置,此處像平面上得到一個最小散焦斑,半徑為 ,將 折算到物平面上得到一個半徑為 的漫散圓斑,用 表示像散的大小,其計算公式為:
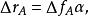 電磁透鏡
電磁透鏡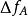 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡式中, 為像散係數,等於磁透鏡出現橢圓度時造成的焦距差; 為孔徑半角。電磁透鏡的像散是可以消除的像差,通常引入一個強度和方位可調的矯正磁場來進行補償,產生這個矯正磁場的裝置稱為消像散器。
色差
色差是由於成像電子的能量不同或波動,電子在透鏡磁場中運動速度不同,從物面上一點散射的電子不能聚焦在像面上同一點而形成的像差,如圖1-6所示。
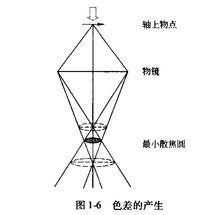 圖1-6
圖1-6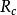 電磁透鏡
電磁透鏡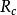 電磁透鏡
電磁透鏡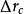 電磁透鏡
電磁透鏡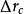 電磁透鏡
電磁透鏡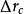 電磁透鏡
電磁透鏡不同能量的電子聚焦在不同位置,像平面上也有一個最小半徑為 的散焦斑。同樣將 折算到物平面上,得到半徑為 的圓斑,用 表示色差, 的大小由下式來確定:
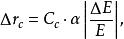 電磁透鏡
電磁透鏡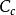 電磁透鏡
電磁透鏡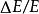 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡式中, 是電磁透鏡的色差係數; 是電子束的能量變化率; 為孔徑半角。上式說明,在色差係數和孔徑半角一定的情況下,電子能量的波動是主要影響因素。引起電子能量波動的原因主要有兩個:一是電子加速電壓不穩,致使入射電子能量波動;二是電子束照射試樣時和試樣相互作用,部分電子產生非彈性散射,致使能量變化。
電磁透鏡的景深和焦長
景深
透鏡的景深是指當像平面固定時(像距不變),在保持圖像清晰的條件下,允許物平面(樣品)沿透鏡主軸平移的最大距離。
 電磁透鏡
電磁透鏡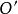 電磁透鏡
電磁透鏡在理想狀態下(不考慮衍射差、球差、像散和色差等影響),由圖1-7可見樣品上某一物點位於 位置時,該點在像平面上應形成一個像點 。
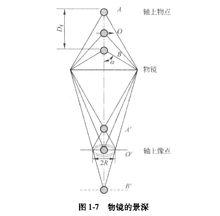 圖1-7
圖1-7 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡當試樣向上方移動,使O點到達A點時,A點的像應位於 處。如果像平面的位置保持不變,則 點將在像平面上散焦成一個半徑為R的圓斑;當試樣向下移動,使原物點O到達B點時,B點將在像平面的 處成像,同樣會形成一個半徑為R的散焦斑。
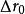 電磁透鏡
電磁透鏡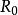 電磁透鏡
電磁透鏡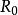 電磁透鏡
電磁透鏡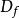 電磁透鏡
電磁透鏡如果衍射效應是決定透鏡解析度的控制因素(即上述諸因素中 為最大),在像平面上由衍射引起的散焦斑半徑應是 ,因此,只要物點在像平面上形成的圓斑半徑R小於或等於 時,像平面上的圖像就仍能保持清晰,所以,樣品在從A到B的範圍內移動時,並不影響物像的清晰度,AB間的這段距離稱為景深,用 表示。
由圖1-7的幾何關係可知:
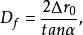 電磁透鏡
電磁透鏡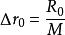 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡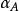 電磁透鏡
電磁透鏡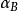 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡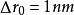 電磁透鏡
電磁透鏡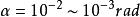 電磁透鏡
電磁透鏡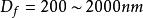 電磁透鏡
電磁透鏡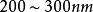 電磁透鏡
電磁透鏡式中, , 為放大倍數; 為孔徑半角。因為電磁透鏡的孔徑半角很小,同時 、 兩點間的距離比透鏡的物距小得多,所以可以認為樣品上的物點 在位於位置 和位置 時,相應的 、 近似地和 相等。如果 , ,求出 。透射電子顯微鏡的金屬薄膜試樣的厚度一般只有 ,因此上述景深範圍可以保證樣品整個厚度範圍內各處細節都清晰可見。
焦長
透鏡的焦長是指固定樣品的條件下(物距不變),像平面沿透鏡主軸平移時仍能保持圖像清晰的最大距離。
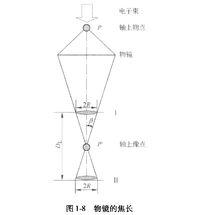 圖1-8
圖1-8 電磁透鏡
電磁透鏡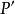 電磁透鏡
電磁透鏡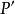 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡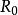 電磁透鏡
電磁透鏡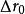 電磁透鏡
電磁透鏡由圖1-8可見,樣品上某一點 通過透鏡後正焦位置應是 點。如果把像平面移動到Ⅰ位置,則 點將散焦成一個半徑為 的欠焦斑;如果把像平面反向移動相等的距離到達位置Ⅱ時,則得到半徑為 的過焦斑。若決定透鏡解析度的控制因素仍是衍射效應,由衍射產生的最小散焦斑直徑等於 ,在物平面上為 ,則根據圖1-8中的幾何關係可以得到:
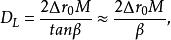 電磁透鏡
電磁透鏡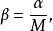 電磁透鏡
電磁透鏡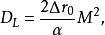 電磁透鏡
電磁透鏡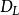 電磁透鏡
電磁透鏡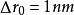 電磁透鏡
電磁透鏡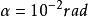 電磁透鏡
電磁透鏡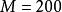 電磁透鏡
電磁透鏡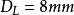 電磁透鏡
電磁透鏡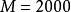 電磁透鏡
電磁透鏡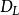 電磁透鏡
電磁透鏡式中, 就是透鏡的焦長。如果 , , 倍,則 。考慮到電子顯微鏡是多級放大,總放大倍數可以很高,如倍時,可達到80cm。這使得在透射電鏡中,螢光屏和照相底片之間的距離可以很大,只要在焦長範圍內就能得到清晰的圖像。
 電磁透鏡
電磁透鏡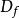 電磁透鏡
電磁透鏡 電磁透鏡
電磁透鏡從計算景深和焦長的公式中可以看到,隨著孔徑半角的減小,和都會變大,因此,在電磁透鏡中插入一個直徑較小的光闌時,可明顯增加景深和焦長。

