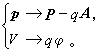簡介
描述電磁場的物理量,包括標勢嗞 和矢勢A兩部分。它在電磁理論中起著十分重要的作用。電磁勢和電磁場(電場強度E和磁感應強度B)之間關係為: 
引進電磁勢後可以將電磁場所滿足的麥克斯韋方程組,化為電磁勢所滿足的一組微分方程,未知量個數和方程個數都減少了,而且,電磁勢與電荷密度 ρ及電流密度j的依賴關係比較簡單直接,易於求解。
麥克斯韋方程組
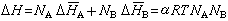
引入矢勢A和標勢嗞後,方程組的第一式和最後一式自然滿足。事實上, 正是由最後一式引出矢勢A,然後再由第一式和矢勢引出標勢嗞的。由電磁勢和電磁場之間關係可以看出,在電磁勢(A,嗞)作下列變換時 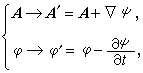
E和B保持不變,式中ψ為任意的標量函式。所以,勢(A,嗞)和勢(A′,嗞┡)描述同一電磁場, 上列變換稱為規範變換。由於(A,嗞)的這種任意性,為了使基本方程和計算簡化,在不同的問題中可以採用不同的輔助條件,即所謂規範條件來選定A和嗞 。套用最廣的是庫侖規範 墷·A=0
和洛倫茲規範 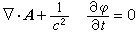 。
。
採用洛倫茲規範時,在真空情形下,可從麥克斯韋方程組得到下列達朗伯方程 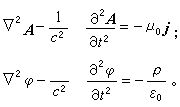
可見在洛倫茲規範下,勢的基本方程化為特別簡單的對稱形式,其物理意義也十分明顯。上兩式的解為推遲勢 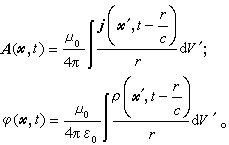
上兩式說明,電荷和電流所產生的物理作用不能夠立刻傳至觀察點,所推遲的時間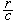 代表電磁作用從電荷電流所在點x′傳至觀察點x所需的時間,ρ和j給定後就可算出推遲勢,再由電磁勢和電磁場的關係式就可求得空間任意點的電磁場。電磁場以有限速度傳播這一點說明能量定域在電磁場中,並從而說明電磁場的物質性。
代表電磁作用從電荷電流所在點x′傳至觀察點x所需的時間,ρ和j給定後就可算出推遲勢,再由電磁勢和電磁場的關係式就可求得空間任意點的電磁場。電磁場以有限速度傳播這一點說明能量定域在電磁場中,並從而說明電磁場的物質性。
帶電粒子在電磁場中受力的洛倫茲公式
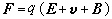 ,
,
也可以用電磁勢來表示:在非相對論情形下,拉格朗日量為 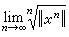 ;
;
而在相對論情形下 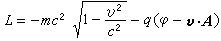 。
。
這時洛倫茲公式就是引用上列拉格朗日量的拉格朗日方程。由上式或前式可知正則動量P為機械動量 p和qA的矢量和,即 P=p+qA。
可以證明,從普通的勢場V過渡到電磁場時,只需將哈密頓量中的機械動量p和勢能V作如下代換即可 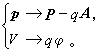
上述結果在量子理論中常會用到。
在量子力學中電磁勢與帶電粒子波函式的位相密切有關。帶電粒子在沒有電磁場的空間中運動時,也會受到電磁勢的作用而改變相位,從而引起可觀察的物理效應,即所謂阿哈羅諾夫-玻姆效應。
從現代規範場理論的角度看,電磁場是以U(1)群為規範群的規範場,而電磁勢就是主纖維叢上的聯絡。
參考書目
曹昌祺著:《電動力學》,人民教育出版社,北京,1979。
郭碩鴻編:《電動力學》,人民教育出版社,北京,1979。
配圖
相關連線

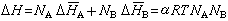
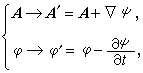
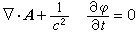 。
。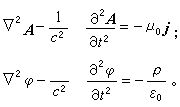
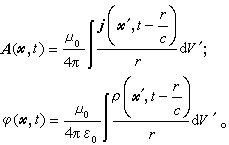
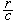 代表電磁作用從電荷電流所在點x′傳至觀察點x所需的時間,ρ和j給定後就可算出推遲勢,再由電磁勢和電磁場的關係式就可求得空間任意點的電磁場。電磁場以有限速度傳播這一點說明能量定域在電磁場中,並從而說明電磁場的物質性。
代表電磁作用從電荷電流所在點x′傳至觀察點x所需的時間,ρ和j給定後就可算出推遲勢,再由電磁勢和電磁場的關係式就可求得空間任意點的電磁場。電磁場以有限速度傳播這一點說明能量定域在電磁場中,並從而說明電磁場的物質性。 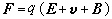 ,
,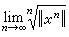 ;
;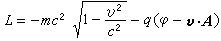 。
。