簡介
 零知識證明
零知識證明在有必要證明一個命題是否正確,又不需要提示與這個命題相關的任何信息時,零知識證明系統(也叫做最小泄露證明系統)是不可或缺的。零知識證明系統包括兩部分:宣稱某一命題為真的示證者(prover)和確認該命題確實為真的驗證者(verifier)。證明是通過這兩部分之間的互動來執行的。在零知識協定的結尾,驗證者只有當命題為真時才會確認。但是,如果示證者宣稱一個錯誤的命題,那么驗證者完全可能發現這個錯誤。這種思想源自互動式證明系統。互動式系統在計算複雜度理論方面已經獲得異常獨立的地位。
零知識證明(Zero—KnowledgeProof)起源於最小泄露證明。設P表示掌握某些信息,並希望證實這一事實的實體,設V是證明這一事實的實體。假如某個協定向V證明P的確掌握某些信息,但V無法推斷出這些信息是什麼,我們稱P實現了最小泄露證明。不僅如此,如果V除了知道P能夠證明某一事實外,不能夠得到其他任何知識,我們稱P實現了零知識證明,相應的協定稱作零知識協定。
性質
在最小泄露協定中零知識證明需要滿足下述兩個性質。
(1)正確性。P無法欺騙V。換言之,若P不知道一個定理的證明方法,則P使V相信他會證明定理的機率很低。
(2)完備性。V無法欺騙P。若P知道一個定理的證明方法,則P使V以絕對優勢的機率相信他能證明。
在零知識協定中,除滿足上述兩個條件以外,還滿足下述的第三個性質。
(3)零知識性。V無法獲取任何額外的知識。
我們把性質(1)和(2)稱為零知識證明的正確性和完備性,而性質(3)稱為零知識性。
屬性
零知識證明需要滿足三個屬性。
1、如果語句為真,誠實的驗證者(即:正確遵循協定的驗證者)將由誠實的證明者確信這一事實。
2、如果語句為假,不排除有機率欺騙者可以說服誠實的驗證者它是真的。
3、如果語句為真,證明者的目的就是向驗證者證明並使驗證者相信自己知道或擁有某一訊息,而在證明過程中不可向驗證者泄漏任何有關被證明訊息的內容。
零知識證明並不是數學意義上的證明,因為它存在小機率的誤差,欺騙者有可能通過虛假陳述騙過證明者。換句話來說,零知識證明是機率證明而不是確定性證明。但是也存在有技術能將誤差降低到可以忽略的值。
零知識的形式定義必須使用一些計算模型,最常見的是圖靈機的計算模型。
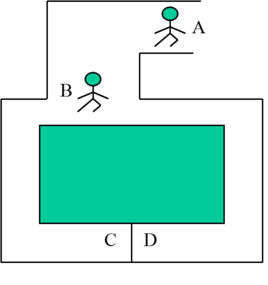
證明舉例
1、A要向B證明自己擁有某個房間的鑰匙,假設該房間只能用鑰匙打開鎖,而其他任何方法都打不開。這時有2個方法:
①A把鑰匙出示給B,B用這把鑰匙打開該房間的鎖,從而證明A擁有該房間的正確的鑰匙。
②B確定該房間內有某一物體,A用自己擁有的鑰匙打開該房間的門,然後把物體拿出來出示給B,從而證明自己確實擁有該房間的鑰匙。
後面的②方法屬於零知識證明。它的好處在於,在整個證明的過程中,B始終不能看到鑰匙的樣子,從而避免了鑰匙的泄露。
2、A擁有B的公鑰,A沒有見過B,而B見過A的照片,偶然一天兩個人見面了,B認出了A,但A不能確定面前的人是否是B,這時B要向A證明自己是B,也有2個方法。
①B把自己的私鑰給A,A用這個私鑰對某個數據加密,然後用B的公鑰解密,如果正確,則證明對方確實是B。
②A給出一個隨機值,並使用B的公鑰對其加密,然後將加密後的數據交給B,B用自己的私鑰解密並展示給A,如果與A給出的隨機值相同,則證明對方是B。
後面的方法屬於零知識證明。
3、有一個缺口環形的長廊,出口和入口距離非常近(在目距之內),但走廊中間某處有一道只能用鑰匙打開的門,A要向B證明自己擁有該門的鑰匙。採用零知識證明,則B看著A從入口進入走廊,然後又從出口走出走廊,這時B沒有得到任何關於這個鑰匙的信息,但是完全可以證明A擁有鑰匙。