簡介
隸屬函式,也稱為歸屬函式或模糊元函式,是模糊集合中會用到的函式,是一般集合中指示函式的一般化。指示函式可以說明一個集合中的元素是否屬於特定子集合。一元素的指示函式的值可能是0或是1,而一元素的隸屬函式會是0到1之間的數值,表示元素屬於某模糊集合的“真實程度”(degree of truth)。
例如質數為一集合,整數3屬於質數,其指示函式為1,整數4不屬於質數,其指示函式為0。但針對模糊集合,可能不會有如此明確的定義,假設胖子是模糊集合,可能體重80公斤的人其隸屬函式為0.9,體重70公斤的人其隸屬函式為0.8。
隸屬函式數值是在0到1之間,看似類似機率,但兩者是不同的概念。
隸屬函式最早是由盧菲特·澤德在1965年第一篇有關模糊集合的論文中提及,他在模糊集合的論文中,提出用值域在0到1之間的隸屬函式,針對定義域中所有的數值定義。
定義
 隸屬函式
隸屬函式 隸屬函式
隸屬函式 隸屬函式
隸屬函式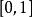 隸屬函式
隸屬函式針對集合 ,集合 上的隸屬函式是將集合 映射到單位實數區間 的函式。
 隸屬函式
隸屬函式 隸屬函式
隸屬函式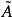 隸屬函式
隸屬函式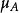 隸屬函式
隸屬函式 隸屬函式
隸屬函式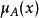 隸屬函式
隸屬函式 隸屬函式
隸屬函式 隸屬函式
隸屬函式 隸屬函式
隸屬函式 隸屬函式
隸屬函式 隸屬函式
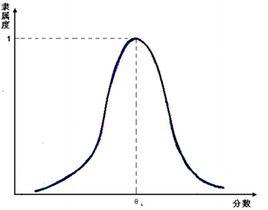
隸屬函式集合上的隸屬函式對應 集合中的模糊子集。對應模糊集合 的隸屬函式一般會用 來表示。針對集合中的元素 , 的數值稱為對應模糊集合 的隸屬度,表示符合模糊集合的程度。0表示元素不是模糊集合的元素,1表示元素是模糊集合的元素,0到1之間的值表示此元素部分符合模糊集合。
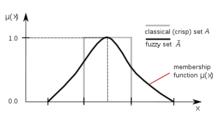 圖1.模糊集合的隸屬函式
圖1.模糊集合的隸屬函式 隸屬函式
隸屬函式 隸屬函式
隸屬函式有時會用一個更通用的定義 ,隸屬函式的值可以是任意的固定代數或是數學結構中取值 ,一般會要求 至少是偏序關係或是格 (數學)。一般值在[0,1]之間的隸屬函式此時會稱為[0,1]-值隸屬函式。
隸屬函式的確定方法
1)模糊統計方法
這個方法藉助了機率統計的中的思想,其步驟與機率統計中的隨機試驗是相對應的。一個模糊統計試驗也要有四個要素:
 隸屬函式
隸屬函式(1)論域;
 隸屬函式
隸屬函式 隸屬函式
隸屬函式(2)試驗所要處理的論域的固定元素;
 隸屬函式
隸屬函式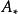 隸屬函式
隸屬函式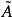 隸屬函式
隸屬函式 隸屬函式
隸屬函式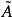 隸屬函式
隸屬函式(3)論域的可變動的子集,他作為模糊集的有可塑性的邊界的反映,可由此得到每次試驗中是否符合所刻劃的模糊概念的一個判決;
 隸屬函式
隸屬函式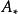 隸屬函式
隸屬函式(4)條件集,它限制著的變化。
模糊統計法是在大量的實驗中確定隸屬函式的方法。模糊統計法包括下列步驟 :
1)確定論域與因素集;
2)要求參與實驗者就論域中各給出的點是否屬於因素集中的各元素進行投票;
3)統計投票結果,求出隸屬函式。
 隸屬函式
隸屬函式 隸屬函式
隸屬函式 隸屬函式
隸屬函式隨著的增大,隸屬頻率也會趨向穩定,這個穩定值就對的隸屬度的值。選此方法較為理想的情況是如果模糊集反映的是社會的一般意識,它的大量的可重複表達的個別意識的平均結果,例如青年人,經濟成長快,生產正常等。
2)指派方法
 隸屬函式
隸屬函式若模糊集定義在實數域上,則模糊集的隸屬函式稱為模糊分布。所謂指派方法,就是根據問題的性質套用現成的某些形式的模糊分布,然後根據測量數據確定分布中所含的參數。
3)專家經驗法
專家經驗法是根據專家的實際經驗給出模糊信息的處理算式或相應權係數值來確定隸屬函式一種方法。在許多情況下,經常是初步確定粗略的隸屬函式,然後再通過“學習”和實踐檢驗逐步修改和完善,而實際效果正是檢驗和調整隸屬函式的依據。選此方法較為理想的情況是:如果模糊集反映的是某個時間段的個別意識,經驗判斷,例如專家對某個項目可行性的評價等。
4)二元對比排序法
對於有些模糊集,很難給出隸屬度,但可以通過對多個事物之間的兩兩對比來確定某種特徵下的順序,由此來決定這些事物對該特徵的隸屬函式的大體形狀。二元對比排序法是一種較實用的確定隸屬度函式的方法。
5)借用已有的“客觀”
尺度選此方法較為理想的情況是模糊集反映的模糊概念已有相應成熟的指標,這種指標經過長期的實踐檢驗已成為公認的對事物的真實的又是本質的描述,則可直接採用這種指標。
套用——容度
隸屬函式的一個套用是在決策理論中的 容度(capacity)。
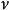 隸屬函式
隸屬函式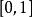 隸屬函式
隸屬函式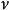 隸屬函式
隸屬函式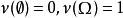 隸屬函式
隸屬函式在決策理論中,容度定義為函式 ,其定義域 S是某個集合的子集,值域為 ,函式 滿足集合定義上的單調而且正規化(也就是 )。這是廣義的機率量測,其中可數可加性的機率公理不一定要成立。容度用來表示某一事件可能性的量測,而特定結果下,其容度的期望值可以對容度作Choquet積分求得。
相關知識
•去模糊化
•模糊量測理論
•模糊集合運算
•粗集合
•模糊控制