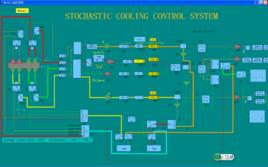
簡介
隨機系統控制的研究成果集中於對系統輸出變數本身的跟蹤，典型的例子是最小方差控制、線性二次型控制（LOG）、具有馬爾柯夫階躍參數系統的隨機控制，等等，控制目標是系統輸出的均值和方差。當系統受高斯噪音影響時，其均值和方差可以決定輸出機率密度函式的形狀。但對於不滿足高斯輸入假設條件的系統，這些方法不能控制輸出機率密度函式的形狀。
傳統的非線性控制的方法主要有以下幾種。一種很典型的方法是在系統的一個名義上的可操作點上設計一個線性狀態反饋控制器，從而達到對非線性系統控制的效果，然而由於每個局部模型只有在一定的可操作範圍內才有效，所以結果只能保證在局部範圍內穩定。另一種方法稱為模糊邏輯控制，這種方法特別適合於那些信息不完全或是對於給定條件不能做出精確控制的模型，因而它在消費品市場和工業過程等方面具有良好的套用。其它的方法，如反饋線性化方法採用微分同胚和非線性反饋將原系統轉化為線性系統。反饋線性化控制是一種常用的非線性控制方法，但它要求系統具有某種預測性質(如系統具有最小相位性、充分光滑、參數精確已知等)，並且往往需要求解複雜的非線性偏微分方程。自適應控制是另一類常用的方法，但其參數更新算法的收斂性和實時性難以得到保證。
控制規律的設計
隨機分布控制研究涉及模型建立、控制器設計、系統分析和故障診斷等很多方面，針對每一個方面中不同類型的問題有不同的解決方法，目前已形成一定體系。下面介紹基於B樣條函式逼近的建模方法及相應的控制規律。
控制問題描述
控制規律的目的在於選擇u（t）使輸出機率密度函式γ（y，u（t））跟蹤給定的機率密度函式g（y），通常採用以下兩類性能指標：
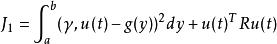隨機系統控制
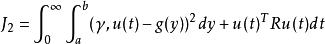隨機系統控制這兩個指標的第一項是關於輸出機率密度函式和給定機率密度函式之間的函式距離量度，第二項為常規的二次型控制向量約束。用這兩個指標的任何一個都可以將控制器的設計轉換為如下的最佳化問題
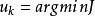隨機系統控制性能指標J和J的不同點在於閉環系統跟蹤性能的差異。一般來說，J的極小化可以實現輸出機率密度函式完全跟蹤給定機率密度函式。
控制算法設計
對離散線性動態系統
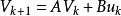隨機系統控制採用線性B樣條模型和二次型性能指標
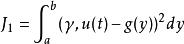隨機系統控制輸出機率密度函式和控制量之間存在如下關係：
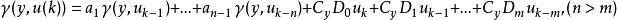隨機系統控制式中，C（y）是關於自由變數y的函式向量，其維數與權向量V一致，是由預先選定的基函式的變換得到的。上述公式包含了兩個部分，其一為機率密度函式之間的自回歸項，其二為關於控制量的滑動平均項。上述公式中的係數a和D以及階次n和m由動態模型式的參數矩陣A，B惟一確定。
在採樣時刻k，γ(y，u)，...，γ(y，u)，u，...u均為已知項，對上述二次型指標直接最佳化，可以得到一個完備的全局最小化解：
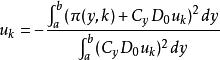隨機系統控制上述公式反映了一個非常重要的負反饋原則，它表明實現機率密度函式形狀控制的最優解依賴於關於輸出機率密度函式的加權積分，這個公式是關於機率密度函式形狀控制的一個最基本的形式，它利用了系統從k-n到k-1時刻的所有可測量信息。由於性能指標是二次型，這個負反饋控制規律的建立在數學上是很容易理解的，在具體實現過程中，還應考慮如何從一組關於輸出分布測量的樣本點來獲取關於輸出機率密度函式的樣本信息，這一過程是非線性的。因此，上述控制規律實際上是一個非線性控制規律，這一點和線性系統二次型指標下通常可獲得的線性負反饋規律是完全不同的，它反映了機率密度函式控制的特殊要求。由上述控制所產生的閉環控制系統也是一個非線性系統，它的穩定性分析只能通過非線性分析的一般方法來進行。當然，如果只考慮權向量所組成的閉環系統，上述的控制規律又是線性的。這又表明，在進行閉環系統穩定性分析的時候，仍可以借用線性系統分析的常規工具來處理權向量的有界性。
實現實時閉環控制可按兩種技術路線進行。第一種是首先利用大量的在k時刻的輸出值來構造關於系統輸出機率密度函式的估計，而後利用公式來直接計算在k時刻的控制量u。這是一個比較簡單的處理辦法。第二種是通過已測量的機率密度函式來合理地計算出B樣條展開的權值，然後直接用這些計算出來的權值產生關於權向量V的反饋控制規律。比較起來，第一條技術路線的計算負荷要比第二條技術路線小。
對於連續型性能指標，除了可以用類似於離散型性能指標的最佳化來設計控制器之外，還可以直接將J和J做為閉環系統的Lyapunov函式。這樣所得到的控制規律應該是使J≤0此外，還可以用無源性的原則來直接設計u(t)。
工業套用
關於輸出機率密度函式閉環控制的討論來自於一些實際系統的控制需要，這裡一方面討論了幾個有代表性的套用前景，另一方面也解釋了在實際工業系統中如何獲得所需的輸出機率密度函式。
1）造紙過程紙張兩維質量分布控制
造紙過程是一個複雜的多變數系統，紙張的質量可由多達近60個物理特性來描述，如紙張的強度、透氣性、透水性等。對控制系統的要求是使這些物理特性符合用戶要求，其中最關鍵的要求是紙張的二維質量分布應儘可能均勻。由於纖維、填料等原材料帶有很強的隨機因素（纖維長度分布、填料分子量分布大小等），這實際上是一個隨機分布控制問題。隨著數字攝像和圖像處理技術的發展，可以直接獲取關於紙張二維質量的灰度分布圖形，進而提取灰度分布的機率密度函式，這樣就間接得到了紙張的質量分布信息，使得控制系統的實現成為可能。這一控制系統的理想機率密度函式是一個定義在指定區間上的均勻分布函式。作者在英國曼徹斯特理工學院的造紙樣機上已經建立了一個簡單的閉環控制系統，並實現了以分布形狀、最小熵和最小方差為目標的多種控制算法。
2）化工過程聚合物分子量分布控制聚合
物的分子量分布是評價聚合物質量的一個重要指標，對化工廠的經濟效益具有重要影響，所以聚合物生產加工對分子量分布控制有很高的要求。聚合物的分子量分布可以用一個機率密度函式表示。影響化工過程聚合物分子量分布的因素眾多，目前主要是通過機理建模的方法得到產品的分子量分布信息。控制系統的主要目的在於選擇控制輸入使描述分子量分布的機率密度函式的形狀跟蹤理想的高聚物產品分子量分布。理想分布是由實驗研究提供的，不同產品的理想分布形狀差別很大，而且具有非對稱和不規則的特點。
3）糧食加工過程糧食加工過程也是一個
典型的隨機分布控制問題，它也是一個複雜的過程控制系統，其關鍵環節由兩個表面上刻有齒狀的滾筒組成。滾筒之間的距離用來控制碾碎顆粒的大小。現有的關於顆粒大小分布的感測器可以直接測量該分布的機率密度函式，因此可以用隨機分布控制規律來實現關於輸出機率密度函式形狀的控制。這一分布控制的意義在於，能夠使加工後的糧食顆粒大小分布服從給定分布，為後續的食品加工工序提供符合要求的原材料，從而提高整個系統的效率及控制質量。
4）燃燒過程燃燒過程是能量轉換和材料
加工過程的一個重要組成部分，它在鋼鐵生產、火力發電和航空發動機中都是一個對控制要求比較高的環節。衡量燃燒過程效益的一個重要指標是燃燒室內溫度場的分布，這種分布按照常規的處理辦法可以通過物理原理建立一組偏微分方程，並利用有限元的計算方法來實現對燃燒室溫度分布場的分析和效益計算，這實際上也是一個隨機分布系統。目前，先進國家已有速度較快的微數字攝像機，由這樣一組攝像機可以組成一定結構的感測器系統，從而獲得燃燒室內火焰分布的三維圖形。這種三維圖形可以用一個聯合機率密度函式來表示，整個系統就成為一個動態的隨機分布系統，控制的目標是通過合理的選擇燃料輸入和過程參數，使火焰分布三維圖形的聯合機率密度函式滿足要求。
