隨機最優控制簡介
隨機最優控制是指選擇控制變數，使隨機系統某個性能指標達到最優的控制。在隨機系統控制中，必須進行狀態估計。套用不同的狀態估計方法，會得到不同的解。因為系統的狀態方程和觀測方程一般都要受到噪聲的干擾，系統的狀態是不確定的，確切知道的只是已經獲得的一組輸出數據和已經施加於系統的控制輸入。如何利用這些輸入輸出數據實時信息去估計系統的狀態或輸出，便構成了不同的信息結構。因此，隨機最優控制問題的研究首先必須與信息結構相聯繫。信息結構分為經典信息結構和非經典信息結構。對於經典信息結構，每一時刻控制量的確定都利用了最大實時信息。而在非經典信息結構下控制量每個分量的確定利用了最大實時信息的一部分。
其次，隨機最優控制問題還必須規定控制策略，即如何利用信息去處理被最佳化的性能指標，從而導致不同類型的控制函式。
開環控制策略是把最佳化性能指標中所有的隨機量用其先驗均值代替，從而簡化為一個確定性的最優控制問題。這樣得到的最優控制是一個開環控制函式
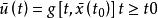隨機最優控制
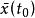隨機最優控制式中 是初始狀態的均值。
閉環控制策略是在動態規劃的每一步都要利用實時信息，控制是信息z(t)的函式
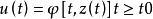隨機最優控制在隨機的情況下，由開環控制策略得到的開環控制函式與由閉環控制策略得到的閉環控制函式，一般是不等價的。通常只有經典信息結構下的閉環最優控制，才是本來意義的最優控制。亦即，利用最大實時信息，並採用閉環控制策略，才能使被最佳化的性能指標在統計意義下達到最優。
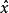隨機最優控制 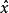隨機最優控制對於線性二次型高斯(LQG)問題，可以由分離原理(也稱分離定理)給出其解析解。最優策略可以由兩部分組成。一部分是個最優濾波器，它按卡爾曼濾波公式求得t時刻的狀態估計 (t|t)。另一部分是按確定型系統最佳化求得最優線性反饋，用狀態估計 (t|t)代替確定型反饋解中的狀態x(t)，得閉環最優解。
隨機控制理論
隨機控制理論的一個主要組成部分是隨機最優控制，這類隨機控制問題的求解有賴於動態規劃的概念和方法。
隨機控制理論的目標是解決隨機控制系統的分析和綜合問題。維納濾波理論和卡爾曼-布希濾波理論是隨機控制理論的基礎。卡爾曼濾波是一種高效率的遞歸濾波器(自回歸濾波器), 它能夠從一系列的不完全及包含噪聲的測量中，估計動態系統的狀態。
控制理論中把隨機過程理論與最優控制理論結合起來研究隨機系統的分支。隨機系統指含有內部隨機參數、外部隨機干擾和觀測噪聲等隨機變數的系統。隨機變數不能用已知的時間函式描述，而只能了解它的某些統計特性。自動控制系統分為確定性系統和不確定性系統兩類，前者可以通過觀測來確定系統的狀態，後者則不能。
隨機系統是不確定性系統的一種，其不確定性是由隨機性引起的。嚴格地說，任何實際的系統都含有隨機因素，但在很多情況下可以忽略這些因素。當這些因素不能忽略時，按確定性控制理論設計的控制系統的行為就會偏離預定的設計要求，而產生隨機偏差量。
隨機控制
隨機控制就是人們對於控制對象的性質一無所知，所必需的條件完全不了解。但對它還要進行有目的的控制，這時能夠採用的唯一的方式就是隨機控制方式。
隨機控制是一種最原始的控制方式，也叫試探性控制。它是其他一切控制方式的基礎。
按照控制的邏輯發展，可將控制分為隨機控制、記憶控制、推理控制和最優控制。
當我們碰到一種棘手的事情，又想不出什麼辦法來解決時，常常硬著頭皮說：“那就碰碰運氣，試試看吧。”“碰運氣”或“試試看”就是最簡單的試探控制。
它是完全建立在偶然機遇的基礎上，是在人們對解決問題所必需的條件不了解，對控制對象的性質不清楚的情況下所能採取的唯一辦法。
例如，我們要打開一個上了鎖的房間，手裡有一大串鑰匙，但不知道其中哪一把能把鎖打開。在這種情況下，人們常用的方法就是“一個一個地試一試看”，直到把鎖打開。
試探控制在成功的同時，常常伴隨著失敗。這種控制方式有較大的風險，對事關重大的活動，一般不宜採用這種控制方式。
在人類社會發展初期，人們的知識十分有限，因而常採用試探控制。但也應該看到，人類對客觀世界的探索是無止境的，無論科學怎樣發達，客觀世界總會存在未被認識的事物，特別是在科學研究中，當人們對某一新領域的研究剛剛開始，還不能用其他方法來控制所研究的對象時，試探控制往往成為人們唯一可以採用的辦法。
最優控制理論
定義
飛機或飛彈在飛行中遇到的陣風，在空間環境中衛星姿態和軌道測量系統中的測量噪聲，各種電子裝置中的噪聲，生產過程中的種種隨機波動等，都是隨機干擾和隨機變數的典型例子。隨機控制系統的套用很廣，涉及航天、航空、航海、軍事上的火力控制系統，工業過程控制，經濟模型的控制，乃至生物醫學等。
最優控制理論（optimal control theory），是現代控制理論的一個主要分支，著重於研究使控制系統的性能指標實現最最佳化的基本條件和綜合方法。 最優控制理論是研究和解決從一切可能的控制方案中尋找最優解的一門學科。它是現代控制理論的重要組成部分。
這方面的開創性工作主要是由貝爾曼（R.E.Bellman）提出的動態規劃和龐特里亞金等人提出的最大值原理。這方面的先期工作應該追溯到維納（N.Wiener）等人奠基的控制論（Cybernetics）。1948年維納發表了題為《控制論—關於動物和機器中控制與通訊的科學》的論文，第一次科學的提出了信息、反饋和控制的概念，為最優控制理論的誕生和發展奠定了基礎。
研究內容
最優控制理論所研究的問題可以概括為：對一個受控的動力學系統或運動過程，從一類允許的控制方案中找出一個最優的控制方案，使系統的運動在由某個初始狀態轉移到指定的目標狀態的同時，其性能指標值為最優。這類問題廣泛存在於技術領域或社會問題中。
例如，確定一個最優控制方式使空間飛行器由一個軌道轉換到另一軌道過程中燃料消耗最少，選擇一個溫度的調節規律和相應的原料配比使化工反應過程的產量最多，制定一項最合理的人口政策使人口發展過程中老化指數、撫養指數和勞動力指數等為最優等，都是一些典型的最優控制問題。最優控制理論是50年代中期在空間技術的推動下開始形成和發展起來的。蘇聯學者Л.С.龐特里亞金1958年提出的極大值原理和美國學者R.貝爾曼1956年提出的動態規劃，對最優控制理論的形成和發展起了重要的作用。線性系統在二次型性能指標下的最優控制問題則是R.E.卡爾曼在60年代初提出和解決的。
分析
使隨機控制系統的某個性能指標泛函取極小值的控制稱為隨機最優控制。由於存在隨機因素，這種性能指標泛函需要表示為統計平均（求數學期望）的形式：
統計平均
式中E{·}表示{·}的均值即數學期望。使性能指標J為極小的最優控制常可取為開環和反饋控制兩種形式。如果控制過程中決定u(t）所依據的只是設計時過程特性和隨機變數的信息，沒有進一步的測量和更新，這種控制策略就稱為是開環的。若在決定t時刻的控制作用u(t）時可以直接利用τ時刻的實時測量值y（τ），則稱控制u(t）具有反饋形式，其中要求τ≤t，這是因果性或物理可實現性所要求的。
按照利用實時信息的充分程度，又可把反饋形式的控制策略分為兩種情形。當只利用這些信息來控制狀態變數，而沒有通過實時觀測來估計和改進各隨機變數的統計特性並修改控制策略時，這種策略稱為是被動反饋式（簡稱反饋式）的。若控制策略兼有上述“控制”和“估計”兩種功能並具有自行修正的能力，則稱為閉環策略（或主動反饋策略）。這種“反饋”和“閉環”的差別是不確定性控制問題所特有的。
A.A.費爾德包姆最先指出閉環隨機最優控制策略的這種雙重功能，並稱之為二重最優控制。閉環（或二重）最優策略可達到在已有信息條件下的最好品質或全局最優解。同時它還具有不斷按照實時測量改進對不確定性的認識並修正策略的功能，也稱為隨機自適應最優控制。閉環最優控制的求解很困難，通常只能根據最優解的定性性質來構造次優解。只對某些特殊問題才可能給出定量解法。
重要性質
隨機最優控制有兩個重要的性質。由於存在不確定性，控制作用常寧可取得弱一些，保守一些。這稱為謹慎控制。另一方面為更好和更快地進行估計，必須不斷激發系統中各種運動模式，為此需要加入一些試探作用。試探作用的大小，則根據增加的誤差、直接費用和所帶來的好處等因素加以折衷權衡進行選擇。謹慎和試探已成為設計隨機控制策略的兩個重要原則。
研究課題
隨機控制理論研究的課題包括隨機系統的結構特性和運動特性（如動態特性、能控性、能觀測性、穩定性）的分析，隨機系統狀態的估計，以及隨機控制系統的綜合（即根據期望性能指標設計控制器）。隨機系統中含有隨機變數，所以在研究中需要使用隨機過程的基本概念和機率統計方法。嚴格實現隨機最優控制是很困難的。
對於線性二次型高斯（LQG）隨機過程控制問題，包括它的特例最小方差控制問題，可以套用分離原理把隨機最優控制問題分解成狀態估計問題和確定性最優控制問題，最終能得到全局最優的結果。但對於一般的隨機控制問題套用分離原理只能得到次優的結果。
主要方法
為了解決最優控制問題，必須建立描述受控運動過程的運動方程，給出控制變數的允許取值範圍，指定運動過程的初始狀態和目標狀態，並且規定一個評價運動過程品質優劣的性能指標。通常，性能指標的好壞取決於所選擇的控制函式和相應的運動狀態。系統的運動狀態受到運動方程的約束，而控制函式只能在允許的範圍內選取。因此，從數學上看，確定最優控制問題可以表述為：在運動方程和允許控制範圍的約束下，對以控制函式和運動狀態為變數的性能指標函式（稱為泛函）求取極值（極大值或極小值）。解決最優控制問題的主要方法有古典變分法、極大值原理和動態規劃。
古典變分法
研究對泛函求極值的一種數學方法。古典變分法只能用在控制變數的取值範圍不受限制的情況。在許多實際控制問題中，控制函式的取值常常受到封閉性的邊界限制，如方向舵只能在兩個極限值範圍內轉動，電動機的力矩只能在正負的最大值範圍內產生等。因此，古典變分法對於解決許多重要的實際最優控制問題，是無能為力的。
極大值原理
極大值原理，是分析力學中哈密頓方法的推廣。極大值原理的突出優點是可用於控制變數受限制的情況，能給出問題中最優控制所必須滿足的條件。
動態規劃
動態規劃是數學規劃的一種，同樣可用於控制變數受限制的情況，是一種很適合於在計算機上進行計算的比較有效的方法。
最優控制理論已被套用於最省燃料控制系統、最小能耗控制系統、線性調節器等。
最佳化技術
最優控制的實現離不開最最佳化技術，最最佳化技術是研究和解決最最佳化問題的一門學科，它研究和解決如何從一切可能的方案中尋找最優的方案。也就是說，最最佳化技術是研究和解決如何將最最佳化問題表示為數學模型以及如何根據數學模型儘快求出其最優解這兩大問題。一般而言，用最最佳化方法解決實際工程問題可分為三步進行：
①根據所提出的最最佳化問題，建立最最佳化問題的數學模型，確定變數，列出約束條件和目標函式；
②對所建立的數學模型進行具體分析和研究，選擇合適的最最佳化方法；
③根據最最佳化方法的算法列出程式框圖和編寫程式，用計算機求出最優解，並對算法的收斂性、通用性、簡便性、計算效率及誤差等作出評價。
求解方法
所謂最最佳化問題，就是尋找一個最優控制方案或最優控制規律，使系統能最優地達到預期的目標。在最最佳化問題的數學模型建立後，主要問題是如何通過不同的求解方法解決尋優問題。一般而言，最最佳化方式有離線靜態最佳化方式和線上動態最佳化方式，而最最佳化問題的求解方法大致可分為四類：
1.解析法
對於目標函式及約束條件具有簡單而明確的數學表達式的最最佳化問題，通常可採用解析法來解決。其求解方法是先按照函式極值的必要條件，用數學分析方法求出其解析解，然後按照充分條件或問題的實際物理意義間接地確定最優解。
這種方法適用於性能指標及約束有明顯解析表達式的情況。其一般步是先用求導方法或變分法求出最優控制的必要條件，得到一組方程或不等式，然後求解這組方程或不等式，得到最優控制的解析解即為所求的最優控制。解析法大致可分為兩大類。第一類，無約束時，採用微分法或變分法。第二類，有約束時，採用極大值原理或動態規劃。
（1）變分法：當控制向量不受約束時，引入哈密頓函式，套用變分法可以導出最優控制的必要條件，即正則方程、控制方程、邊界條件、橫截條件。
（2）極大值原理：在用變分法求解最優控制問題時，是假定控制向量u(O)不受任何限制，即容許控制集合可以看成是整個P維控制空間開集，控制變分u是任意的，同時還要求哈密頓出數H對u連續可微，但在實際工程上，控制變數往往受到一定的限制，這時可以用極大值原理來求解最優控制問題，這種方法其實是由變分法引申而來的，但由於它能套用於控制變數u(t)受邊界限制的情況，並且不要求哈密頓出數H對u連續可微，因此獲得了廣泛的套用。
（3）動態規劃：極大值原理一樣，是處理控制向量限制在一定閉集內的最優控制問題的有效數學方法，它把複雜的最優控制間題變為多級決策過程的遞推函式關係，其基礎和核心時最優性原理即在一個多級決策問題中無論初始狀態和初始決策如何，當把其中的任何一級和狀態再作為初始級和初始狀態時，如下的決定對與這一級開始往後的多級決策過程的一部分必定仍然是一個最優決策。因此，利用這一最優性原理必然可把一個多級決策問題化為最優的單級決策問題並且本級決策與本級以前的任何決策無關，只與本級的初始位置和初始決策有關。對於連續系統用動態規劃法求最優控制問題時，可以先把連續系統離散化，用有限差分方程近似代替連續方程，然後用離散動態規劃法求解。
2.數值解法（直接法）
對於目標函式較為複雜或無明確的數學表達式或無法用解析法求解的最最佳化問題，通常可採用直接法來解決。直接法的基本思想，就是用直接搜尋方法經過一系列的疊代以產生點的序列，使之逐步接近到最優點。直接法常常是根據經驗或實驗而得到的。
性能指標比較複雜或不能用變數顯函式表示時，可以採用直接搜尋法，經過若干次疊代搜尋到最優點，數值計算法可以分為兩大類：
（1）區間消去法，又稱為一維搜尋法，適用於求解單變數極值問題。主要有黃金分割法、多項式插值法等。
（2）爬山法，又稱多維搜尋法，適用於求解多變數極值問題。主要有坐標輪轉法、步長加速法等。
3.解析與數值相結合的尋優方法（梯度型法）
是一種解析與數值計算相結合的方法。主要包括兩大類：一種是無約束梯度法，如陡降法、擬牛頓法等。第二類是有約束梯度法，如可行方向法、梯度投影法。
4.網路最最佳化方法
這種方法以網路圖作為數學模型，用圖論方法進行搜尋的尋優方法。
